题目内容
 正方形和圆都是人们比较喜欢的图形,给人以美得感受.我校数学兴趣小组在研究性学习中发现:
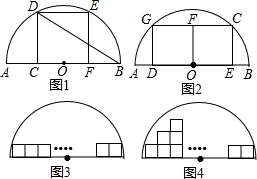
正方形和圆都是人们比较喜欢的图形,给人以美得感受.我校数学兴趣小组在研究性学习中发现:(1)在如图1中研究以AB为直径的半圆中,裁剪出面积最大的正方形CDEF时惊喜地发现,点C和F其实分别是线段AF和BC的黄金分割点!如果设圆的半径为r,此时正方形的边长a1=
(2)如果在半径为r的半圆中裁剪出两个同样大小且分别面积最大的正方形的边长a2=
(3)当n=9时,我们还可以在第一层的上面再裁剪出同样大小的正方形,也可以再在第二层的上面再裁剪出第三层同样大小的正方形,问最多可以裁剪到第几层?
考点:圆的综合题
专题:
分析:(1)根据直角三角形的射影定理可以求得边长a1,再利用tan∠ABD=
求出即可;
(2)根据直角三角形的射影定理可以求得边长a2,进而得出边长an;
(3)通过观察排列的规律即可判断.
| CD |
| BC |
(2)根据直角三角形的射影定理可以求得边长a2,进而得出边长an;
(3)通过观察排列的规律即可判断.
解答:解:(1)由于点C和点F其实分别是线段AF和的BC黄金分割点.
所以a12=(r+
)(r-
),
解得:a1=
r;
tan∠ABD=
=
=
,
故答案为:
r,
;
(2)根据题意得:a22=(r+a2)(r-a2),
解得a2=
r;
=(r+
an)(r-
an),
解得an=(2
)r;
故答案为:
r,(2
)r;
(3)当n=9时,我们还可以在第一层的上面再裁剪出同样大小7个正方形,
再在第二层的上面再裁剪出第三层同样大小5正方形,依此类推,4层是3个,5层1个;
所以最多可以裁剪到第5层.
所以a12=(r+
| a1 |
| 2 |
| a1 |
| 2 |
解得:a1=
2
| ||
| 5 |
tan∠ABD=
| CD |
| BC |
| ||||
r+
|
| ||
| 2 |
故答案为:
2
| ||
| 5 |
| ||
| 2 |
(2)根据题意得:a22=(r+a2)(r-a2),
解得a2=
| ||
| 2 |
| a | 2 n |
| 1 |
| n |
| 1 |
| n |
解得an=(2
|
故答案为:
| ||
| 2 |
|
(3)当n=9时,我们还可以在第一层的上面再裁剪出同样大小7个正方形,
再在第二层的上面再裁剪出第三层同样大小5正方形,依此类推,4层是3个,5层1个;
所以最多可以裁剪到第5层.
点评:本题考查了直角三角形的射影定理的运用、圆的圆周角定理和锐角三角函数关系等知识,利用射影定理得出是解题关键.

练习册系列答案
相关题目
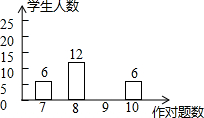 数学老师布置10道选择题当堂测试,统计结果每人至少答对7道题,数学课代表对全班48名同学的答题情况绘制了条形统计图.
数学老师布置10道选择题当堂测试,统计结果每人至少答对7道题,数学课代表对全班48名同学的答题情况绘制了条形统计图.
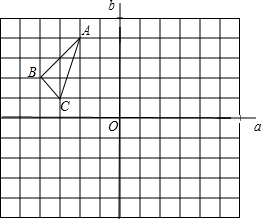 在一个网格图中有一个△ABC,直线a,b相交于点O,(不留作图痕迹但请标记出对应点的字母)
在一个网格图中有一个△ABC,直线a,b相交于点O,(不留作图痕迹但请标记出对应点的字母) 如图,AE,AD分别是△ABC的高和角平分线,且∠B=30°,∠C=70°.
如图,AE,AD分别是△ABC的高和角平分线,且∠B=30°,∠C=70°. 已知等腰△ABC中,AB=AC,一腰上的中线BD把这个△ABC的周长分成15cm和6cm两部分,求这个等腰三角形的各边长?(提示:用方程思想解决)
已知等腰△ABC中,AB=AC,一腰上的中线BD把这个△ABC的周长分成15cm和6cm两部分,求这个等腰三角形的各边长?(提示:用方程思想解决)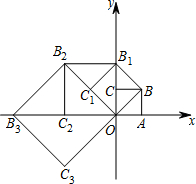 如图,在平面直角坐标系中有一个边长为1的正方形OABC,边OA,OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,…,照此规律作下去,则点B2的坐标为
如图,在平面直角坐标系中有一个边长为1的正方形OABC,边OA,OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,…,照此规律作下去,则点B2的坐标为 如图,函数y=kx(k≠0)和y=ax+4(a≠0)的图象相交于点A(2,3),则不等式kx>ax+4的解集为
如图,函数y=kx(k≠0)和y=ax+4(a≠0)的图象相交于点A(2,3),则不等式kx>ax+4的解集为