题目内容
如图,已知抛物线y=-
x2+
x+8与x轴交于A,B两点,与y轴交于C点.
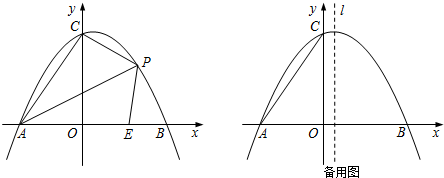
(1)求A,B,C三点坐标及该抛物线的对称轴;
(2)若点E在x轴上,点P(x,y)是抛物线在第一象限上的点,△APC≌△APE,求E,P两点坐标;
(3)在抛物线对称轴上是否存在点M,使得∠AMC是钝角?若存在,求出点M的纵坐标n的取值范围;若不存在,请说明理由.
| 1 |
| 6 |
| 1 |
| 3 |
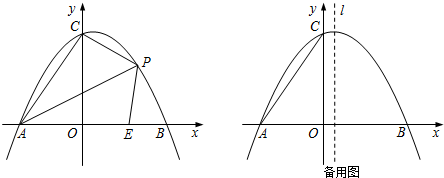
(1)求A,B,C三点坐标及该抛物线的对称轴;
(2)若点E在x轴上,点P(x,y)是抛物线在第一象限上的点,△APC≌△APE,求E,P两点坐标;
(3)在抛物线对称轴上是否存在点M,使得∠AMC是钝角?若存在,求出点M的纵坐标n的取值范围;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)令x=0,求出点C的坐标,令y=0求出点A和点B的坐标.
(2)连接AP交OC于F点,设F(0,t),连接EF,由△APC≌△APE,得出AE=AC,得出OE的长即可得出点E坐标,由对称性得EF=CF,利用勾股定理求出t,确定点F的坐标,可求得直线AF的表达式,与抛物线联立得出点P的坐标.
(3)作辅助线以AC为直径画⊙N,交对称轴l于S,T,作NQ⊥l于Q,NQ交y轴于J,连接NS,易得点N的坐标,可求出NQ,NS的长,由勾股定理得SQ,即可得到S,T的坐标,
由圆的知识可得出点M在S,T之间时得∠AMC是钝角.所以得出点M的纵坐标n的取值范围.
(2)连接AP交OC于F点,设F(0,t),连接EF,由△APC≌△APE,得出AE=AC,得出OE的长即可得出点E坐标,由对称性得EF=CF,利用勾股定理求出t,确定点F的坐标,可求得直线AF的表达式,与抛物线联立得出点P的坐标.
(3)作辅助线以AC为直径画⊙N,交对称轴l于S,T,作NQ⊥l于Q,NQ交y轴于J,连接NS,易得点N的坐标,可求出NQ,NS的长,由勾股定理得SQ,即可得到S,T的坐标,
由圆的知识可得出点M在S,T之间时得∠AMC是钝角.所以得出点M的纵坐标n的取值范围.
解答:解:(1)把x=0代入y=-
x2+
x+8,得y=8,所以C(0,8).
由-
x2+
x+8=0,解得x=-6,或x=8.
所以点A坐标为(-6,0),点B坐标为(8,0).
所以抛物线的对称轴方程是直线x=1.
(2)如图1,连接AP交OC于F点,设F(0,t),连接EF,

由题意可得AC=10,
∵△APC≌△APE,
∴AE=AC=10,AP平分∠CAE.
∴OE=10-6=4,点E坐标为(4,0).
∵AP平分∠CAE,
∴由对称性得EF=CF=8-t.
在Rt△EOF中,OE2+OF2=EF2,
∴42+t2=(8-t)2,解得t=3.
∴点F坐标为(0,3).
设直线AF的表达式y=kx+b(k≠0),
将点A(-6,0),F(0,3)代入,解得
,
∴直线AF的表达式y=
x+3.
由
,
解得
或
(不符合题意,舍去).
∴P(5,
),E(4,0).
(3)如图2,以AC为直径画⊙N,交对称轴l于S,T,作NQ⊥l于Q,NQ交y轴于J,连接NS,
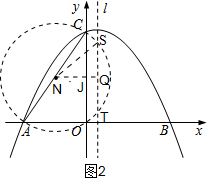
∵C(0,8),点A坐标为(-6,0),N为AC的中点,
∴N为(-3,4),
∵抛物线的对称轴方程是直线x=1.
∴NQ=4,NS=5;
在Rt△SNQ中由勾股定理得SQ=3,
∴S,T的坐标分别为(1,7)和(1,1),
当M介于S和t之间时,延长AM交⊙N于L,∠ALC=90°,
∠AMC>∠ALC,
∴∠AMC是钝角,
∴1<n<7,
∴点M的纵坐标n的取值范围1<n<7.
| 1 |
| 6 |
| 1 |
| 3 |
由-
| 1 |
| 6 |
| 1 |
| 3 |
所以点A坐标为(-6,0),点B坐标为(8,0).
所以抛物线的对称轴方程是直线x=1.
(2)如图1,连接AP交OC于F点,设F(0,t),连接EF,

由题意可得AC=10,
∵△APC≌△APE,
∴AE=AC=10,AP平分∠CAE.
∴OE=10-6=4,点E坐标为(4,0).
∵AP平分∠CAE,
∴由对称性得EF=CF=8-t.
在Rt△EOF中,OE2+OF2=EF2,
∴42+t2=(8-t)2,解得t=3.
∴点F坐标为(0,3).
设直线AF的表达式y=kx+b(k≠0),
将点A(-6,0),F(0,3)代入,解得
|
∴直线AF的表达式y=
| 1 |
| 2 |
由
|
解得
|
|
∴P(5,
| 11 |
| 2 |
(3)如图2,以AC为直径画⊙N,交对称轴l于S,T,作NQ⊥l于Q,NQ交y轴于J,连接NS,

∵C(0,8),点A坐标为(-6,0),N为AC的中点,
∴N为(-3,4),
∵抛物线的对称轴方程是直线x=1.
∴NQ=4,NS=5;
在Rt△SNQ中由勾股定理得SQ=3,
∴S,T的坐标分别为(1,7)和(1,1),
当M介于S和t之间时,延长AM交⊙N于L,∠ALC=90°,
∠AMC>∠ALC,
∴∠AMC是钝角,
∴1<n<7,
∴点M的纵坐标n的取值范围1<n<7.
点评:本题主要考查了二次函数与方程、几何知识的综合应用,涉及全等三角形的性质,一次函数解析式及圆的有关知识.解题的关键是正确作出辅助线,灵活运用二次函数与方程、几何知识的结合.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
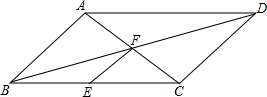 如图,在平行四边形ABCD中,F是对角线的交点,E是边BC的中点,连接EF.
如图,在平行四边形ABCD中,F是对角线的交点,E是边BC的中点,连接EF.
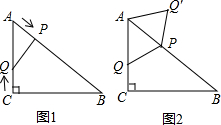 如图1,Rt△ABC中,AC=6cm,BC=8cm,点P以2cm/s的速度从A处沿AB方向匀速运动,点Q以1cm/s的速度从C处沿CA方向匀速运动.连接PQ,若设运动的时间为t(s)(0<t<5).解答下列问题:
如图1,Rt△ABC中,AC=6cm,BC=8cm,点P以2cm/s的速度从A处沿AB方向匀速运动,点Q以1cm/s的速度从C处沿CA方向匀速运动.连接PQ,若设运动的时间为t(s)(0<t<5).解答下列问题: