题目内容
如图1,在平面直角坐标系中,直线y=-
x+4分别交x、y轴于A、B两点,将△AOB沿直线y=kx-
k(k>0)折叠,使B点落在y轴的C点处.
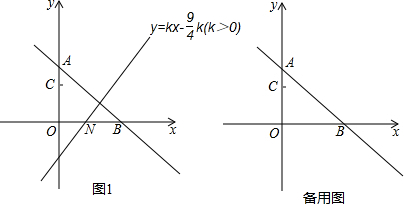
(1)求C点坐标;
(2)若点D沿射线BA运动,连接OD,当△CDB与△CDO面积相等时,求直线OD的解析式;
(3)在(2)的条件下,点D在第一象限,沿x轴平移直线OD,分别交x,y轴于点E,F,在平面直角坐标系中,是否存在点M(m,3)和点P,使四边形EFMP为正方形?若存在,求出点P的坐标;若不存在,说明理由.
| 2 |
| 3 |
| 9 |
| 4 |
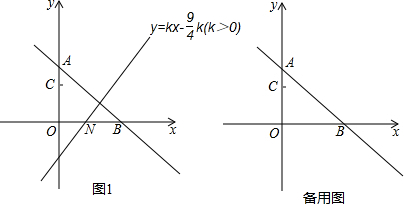
(1)求C点坐标;
(2)若点D沿射线BA运动,连接OD,当△CDB与△CDO面积相等时,求直线OD的解析式;
(3)在(2)的条件下,点D在第一象限,沿x轴平移直线OD,分别交x,y轴于点E,F,在平面直角坐标系中,是否存在点M(m,3)和点P,使四边形EFMP为正方形?若存在,求出点P的坐标;若不存在,说明理由.
考点:一次函数综合题
专题:压轴题
分析:(1)求出点A、B的坐标,设直线y=kx-
k交x轴、y轴于点E、F,求出点E、F的坐标,设BC与直线y=kx-
k交于点G,根据折叠的性质求出点G的横坐标,代入直线求出点G的纵坐标,再根据∠OBC和∠OFE的正切值相等列方程求解得到点G的坐标,然后求解即可;
(2)分①点D在第一象限时,根据等底等高的三角形的面积相等可知点D的纵坐标与点C的纵坐标相等,然后代入直线解析式求出横坐标,从而得到点D的坐标,再写出直线解析式即可;②点D在第二象限时,求出AC的长,再设点D到y轴的距离为a,根据S△CDB=S△ACD+S△ABC列式整理,再根据△CDB与△CDO面积相等列出方程求出a,然后求出点D的坐标,再写出直线OD的解析式即可;
(3)根据平行直线的解析式的k值相等设平移后的直线的解析式为y=2x+b,然后用b表示出OE、OF,过点M作MN⊥y轴于N,过点P作PQ⊥x轴于Q,△MNF、△FOE、△EQP是全等三角形,根据根据全等三角形对应角相等可得MN=OF=EQ,NF=OE=PQ,然后根据点M的纵坐标为3列出方程求出b值,再求出OE、OF,然后求出OQ、PQ,写出点P的坐标即可.
| 9 |
| 4 |
| 9 |
| 4 |
(2)分①点D在第一象限时,根据等底等高的三角形的面积相等可知点D的纵坐标与点C的纵坐标相等,然后代入直线解析式求出横坐标,从而得到点D的坐标,再写出直线解析式即可;②点D在第二象限时,求出AC的长,再设点D到y轴的距离为a,根据S△CDB=S△ACD+S△ABC列式整理,再根据△CDB与△CDO面积相等列出方程求出a,然后求出点D的坐标,再写出直线OD的解析式即可;
(3)根据平行直线的解析式的k值相等设平移后的直线的解析式为y=2x+b,然后用b表示出OE、OF,过点M作MN⊥y轴于N,过点P作PQ⊥x轴于Q,△MNF、△FOE、△EQP是全等三角形,根据根据全等三角形对应角相等可得MN=OF=EQ,NF=OE=PQ,然后根据点M的纵坐标为3列出方程求出b值,再求出OE、OF,然后求出OQ、PQ,写出点P的坐标即可.
解答: 解:(1)令x=0,则y=4,
解:(1)令x=0,则y=4,
令y=0,则-
x+4=0,
解得x=6,
所以,A(0,4),B(6,0),
设直线y=kx-
k交x轴、y轴于点E、F,
则E(
,0),F(0,-
k),
设BC与直线y=kx-
k交于点G,
则点G的横坐标为
=3,
代入直线y=-
x+4得,点G的纵坐标y=
k,
∵∠OBC+∠OCB=∠OFE+∠OCB=90°,
∴∠OBC=∠OFE,
∵tan∠OBC=
=
k,tan∠OFE=
=
=
,
∴
k=
,
解得k=2,k=-2(舍去),
∴点G的坐标为(3,
),
∵点B、C关于 点G对称,
∴点C的坐标为(0,3);
(2)①点D在第一象限时,
∵△CDB与△CDO面积相等,
∴CD∥OB,
∴点D的纵坐标为3,
当y=3时,-
×x+4=3,
解得x=
,
∴点D的坐标为(
,3),
∴直线OD的解析式为y=2x;
②点D在第二象限时,AC=4-3=1,
设点D到y轴的距离为a,
则S△CDB=S△ACD+S△ABC
=
×1•a+
×1×6
=
a+3,
∵△CDB与△CDO面积相等,
∴
a+3=
×3a,
解得a=3,
∴点D的横坐标为-3,
当x=-3时,y=-
×(-3)+4=2+4=6,
∴点D的坐标为(-3,6),
∴直线OD的解析式为y=-2x;
(3)设OD平移后的解析式为y=2x+b,
令y=0,则2x+b=0,
解得x=-
,
令x=0,则y=b,
所以,OE=
,OF=b,
过点M作MN⊥y轴于N,过点P作PQ⊥x轴于Q,
∵四边形EFMP是正方形,
∴易证△MNF≌△FOE≌△EQP,
∴MN=OF=EQ,NF=OE=PQ,
∵M(m,3),
∴ON=b+
=3,
解得b=2,
∴OE=1,OF=2,
∴OQ=OE+QE=1+2=3,
∴点M(-2,3),点P(-3,1),
故,存在点M(-2,3)和点P(-3,1),使四边形EFMP为正方形.
 解:(1)令x=0,则y=4,
解:(1)令x=0,则y=4,令y=0,则-
| 2 |
| 3 |
解得x=6,
所以,A(0,4),B(6,0),
设直线y=kx-
| 9 |
| 4 |
则E(
| 9 |
| 4 |
| 9 |
| 4 |
设BC与直线y=kx-
| 9 |
| 4 |
则点G的横坐标为
| 0+6 |
| 2 |
代入直线y=-
| 2 |
| 3 |
| 3 |
| 4 |
∵∠OBC+∠OCB=∠OFE+∠OCB=90°,
∴∠OBC=∠OFE,
∵tan∠OBC=
| ||
| 6-3 |
| 1 |
| 4 |
| OE |
| OF |
| ||
|
| 1 |
| k |
∴
| 1 |
| 4 |
| 1 |
| k |
解得k=2,k=-2(舍去),
∴点G的坐标为(3,
| 3 |
| 2 |
∵点B、C关于 点G对称,
∴点C的坐标为(0,3);
(2)①点D在第一象限时,
∵△CDB与△CDO面积相等,

∴CD∥OB,
∴点D的纵坐标为3,
当y=3时,-
| 2 |
| 3 |
解得x=
| 3 |
| 2 |
∴点D的坐标为(
| 3 |
| 2 |
∴直线OD的解析式为y=2x;
②点D在第二象限时,AC=4-3=1,
设点D到y轴的距离为a,
则S△CDB=S△ACD+S△ABC
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
∵△CDB与△CDO面积相等,
∴
| 1 |
| 2 |
| 1 |
| 2 |
解得a=3,
∴点D的横坐标为-3,
当x=-3时,y=-
| 2 |
| 3 |
∴点D的坐标为(-3,6),
∴直线OD的解析式为y=-2x;
(3)设OD平移后的解析式为y=2x+b,
令y=0,则2x+b=0,
解得x=-
| b |
| 2 |
令x=0,则y=b,

所以,OE=
| b |
| 2 |
过点M作MN⊥y轴于N,过点P作PQ⊥x轴于Q,
∵四边形EFMP是正方形,
∴易证△MNF≌△FOE≌△EQP,
∴MN=OF=EQ,NF=OE=PQ,
∵M(m,3),
∴ON=b+
| b |
| 2 |
解得b=2,
∴OE=1,OF=2,
∴OQ=OE+QE=1+2=3,
∴点M(-2,3),点P(-3,1),
故,存在点M(-2,3)和点P(-3,1),使四边形EFMP为正方形.
点评:本题是一次函数综合题型,主要利用了直线与坐标轴的交点的求法,轴对称的性质,锐角三角函数的定义,三角形的面积,正方形的性质,全等三角形的判定与性质,难点在于(1)根据等角的正切列出方程,(2)根据点D的位置分情况讨论,(3)作辅助线构造出全等三角形并根据点M的纵坐标列出方程.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
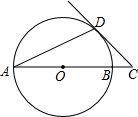 如图,AB是⊙O的直径,AD是弦,∠A=22.5°,延长AB到点C,使得∠ACD=45°.
如图,AB是⊙O的直径,AD是弦,∠A=22.5°,延长AB到点C,使得∠ACD=45°.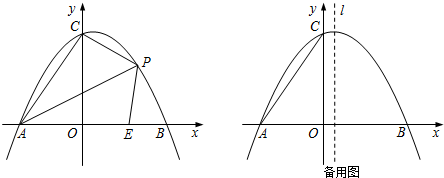
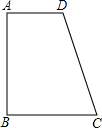 如图,已知AD∥BC,AB⊥BC,AD=2,BC=3,AB=4.
如图,已知AD∥BC,AB⊥BC,AD=2,BC=3,AB=4.