题目内容
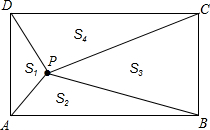 如图,P是矩形ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4,给出如下结论:①S1+S2=S3+S4,②S2+S4=S1+S3,③若S3=2S1,则S4=2S2,正确的结论的序号是
如图,P是矩形ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4,给出如下结论:①S1+S2=S3+S4,②S2+S4=S1+S3,③若S3=2S1,则S4=2S2,正确的结论的序号是考点:矩形的性质
专题:
分析:根据矩形的对边相等可得AB=CD,AD=BC,设点P到AB、BC、CD、DA的距离分别为h1、h2、h3、h4,然后利用三角形的面积公式列式整理即可判断出②正确.
解答: 解:如右图,过点P分别作PF⊥AD于点F,PE⊥AB于点E,
解:如右图,过点P分别作PF⊥AD于点F,PE⊥AB于点E,
∵△APD以AD为底边,△PBC以BC为底边,
∴此时两三角形的高的和为AB,即可得出S1+S3=
矩形ABCD面积;
同理可得出S2+S4=
矩形ABCD面积;
∴②S2+S4=S1+S3正确;
当点P在矩形的两条对角线的交点时,S1+S2=S3+S4.但P是矩形ABCD内的任意一点,所以该等式不一定成立.故①不一定正确;
③若S3=2S1,只能得出△APD与△PBC高度之比,S4不一定等于2S2;故此选项错误;
故答案为:②.
 解:如右图,过点P分别作PF⊥AD于点F,PE⊥AB于点E,
解:如右图,过点P分别作PF⊥AD于点F,PE⊥AB于点E,∵△APD以AD为底边,△PBC以BC为底边,
∴此时两三角形的高的和为AB,即可得出S1+S3=
| 1 |
| 2 |
同理可得出S2+S4=
| 1 |
| 2 |
∴②S2+S4=S1+S3正确;
当点P在矩形的两条对角线的交点时,S1+S2=S3+S4.但P是矩形ABCD内的任意一点,所以该等式不一定成立.故①不一定正确;
③若S3=2S1,只能得出△APD与△PBC高度之比,S4不一定等于2S2;故此选项错误;
故答案为:②.
点评:本题考查了矩形的性质,三角形的面积,以及矩形对角线上点的判定,用矩形的面积表示出相对的两个三角形的面积的和是解题的关键,也是本题的难点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在矩形ABCD中,把∠D沿AE折叠,使点D落在BC边上的点F处,已知∠BAF=60°,则∠DAE的度数是( )
如图,在矩形ABCD中,把∠D沿AE折叠,使点D落在BC边上的点F处,已知∠BAF=60°,则∠DAE的度数是( )| A、15° | B、30° |
| C、45° | D、60° |
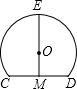 如图,M是CD中点,EM⊥CD,若CD=6,EM=9,则C、E、D三点的所在圆的半径为
如图,M是CD中点,EM⊥CD,若CD=6,EM=9,则C、E、D三点的所在圆的半径为 一次函数y=kx+b的图象如图,当y<0时,x的取值范围是
一次函数y=kx+b的图象如图,当y<0时,x的取值范围是