题目内容
10. 已知:如图,在?ABCD中,点E在BC边上,连接AE,O为AE中点,连接BO并延长交AD于F.
已知:如图,在?ABCD中,点E在BC边上,连接AE,O为AE中点,连接BO并延长交AD于F.(1)求证:△AOF≌△EOB;
(2)当AE平分∠BAD时,四边形ABEF是什么特殊四边形?并证明你的结论.
分析 (1)根据平行四边形的定义可得AD∥BC,进而可得∠FAE=∠AEB,∠AFO=∠EBO,再由O为AE中点可得AO=EO,然后可利用AAS判定:△AOF≌△EOB;
(2)首先证明四边形ABEF是平行四边形,然后再证明AB=AF可得四边形ABEF是菱形.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠FAE=∠AEB,∠AFO=∠EBO,
∵O为AE中点,
∴AO=EO,
在△AOF和△EOB中,$\left\{\begin{array}{l}{∠FAO=∠BEO}\\{∠AFO=∠EBO}\\{AO=EO}\end{array}\right.$,
∴△AOF≌△EOB(AAS);
(2)解:四边形ABEF是菱形;
∵△AOF≌△EOB,
∴AF=BE,
∵AD∥BC,
∴AF∥BE,
∴四边形ABEF是平行四边形,
∴AE平分∠BAD,
∴∠ABF=∠EBF,
∵∠AFO=∠EBO,
∴∠ABO=∠AFO,
∴AF=AB,
∴四边形ABEF是菱形.
点评 此题主要考查了菱形的判定,以及平行四边形的性质,全等三角形的判定和性质,关键是掌握平行四边形对边平行,一组邻边相等的平行四边形是菱形.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
1.点M为数轴上表示-2的点,将点M沿数轴向右平移5个单位到点N,则点N表示的数是( )
| A. | 3 | B. | 5 | C. | -7 | D. | 3或-7 |
19.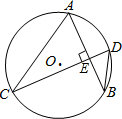 如图,AB、CD是⊙O弦,且AB⊥CD,若∠CDB=50°,则∠ACD的大小为( )
如图,AB、CD是⊙O弦,且AB⊥CD,若∠CDB=50°,则∠ACD的大小为( )
 如图,AB、CD是⊙O弦,且AB⊥CD,若∠CDB=50°,则∠ACD的大小为( )
如图,AB、CD是⊙O弦,且AB⊥CD,若∠CDB=50°,则∠ACD的大小为( )| A. | 30° | B. | 35° | C. | 40° | D. | 50° |
 如图,在笔直的公路L的同侧有A、B两个村庄,已知A、B两村分别到公路的距离AC=3km,BD=4km.现要在公路上建一个汽车站P,使该车站到A、B两村的距离相等,
如图,在笔直的公路L的同侧有A、B两个村庄,已知A、B两村分别到公路的距离AC=3km,BD=4km.现要在公路上建一个汽车站P,使该车站到A、B两村的距离相等,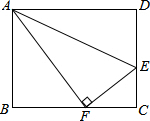 如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE翻折,点D的对称点F恰好落在BC上,已知AD=20cm,AB=16cm,那么折痕AE的长为10$\sqrt{5}$.
如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE翻折,点D的对称点F恰好落在BC上,已知AD=20cm,AB=16cm,那么折痕AE的长为10$\sqrt{5}$.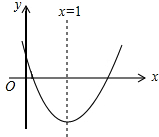 已知二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1,下列结论中:①abc>0;②2a+b=0;③b2-4ac<0;④4a+2b+c>0;⑤3b<2c,其中正确的个数( )
已知二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1,下列结论中:①abc>0;②2a+b=0;③b2-4ac<0;④4a+2b+c>0;⑤3b<2c,其中正确的个数( )