题目内容
15.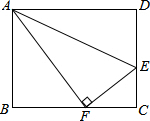 如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE翻折,点D的对称点F恰好落在BC上,已知AD=20cm,AB=16cm,那么折痕AE的长为10$\sqrt{5}$.
如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE翻折,点D的对称点F恰好落在BC上,已知AD=20cm,AB=16cm,那么折痕AE的长为10$\sqrt{5}$.
分析 先在RT△ABF中利用勾股定理求出线段BF,设DE=EF=x,在RTEFC中利用勾股定理求出X,最后在RT△ADE中求出AE即可.
解答  解:∵四边形ABCD是矩形,
解:∵四边形ABCD是矩形,
∴AB=CD=16,AD=BC=20,∠B=∠D=90°,
∵△AEF是由△ADE翻折,
∴AD=AF=20,DE=EF,设DE=EF=x,
在RT△ABF中,∵AB=16.,AF=20,
∴BF=$\sqrt{A{F}^{2}-A{B}^{2}}$=$\sqrt{2{0}^{2}-1{6}^{2}}$=12,
∴FC=BC-BF=20-12=8,
在RT△EFC中,∵EF=x,EC=16-x,FC=8,
∴x2=(16-x)2+82,
∴X=10,
在RT△ADE中,∵AD=20,DE=10,
∴AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=$\sqrt{2{0}^{2}+1{0}^{2}}$=10$\sqrt{5}$.
故答案为10$\sqrt{5}$.
点评 本题考查矩形的性质、翻折不变性、勾股定理等知识,解题的关键是在三个直角三角形中利用勾股定理解决问题,属于中考常考题型.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
20.下列各式中代数式的个数有( )
3x-1,a=4,S=100t+5,5xy-3,4mn,2-b>6,-2,7x2+8x-1.
3x-1,a=4,S=100t+5,5xy-3,4mn,2-b>6,-2,7x2+8x-1.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4. 如图,在平面直角坐标系中,有两条抛物线,它们的对称轴相同,则下列关系中,不正确的是( )
如图,在平面直角坐标系中,有两条抛物线,它们的对称轴相同,则下列关系中,不正确的是( )
 如图,在平面直角坐标系中,有两条抛物线,它们的对称轴相同,则下列关系中,不正确的是( )
如图,在平面直角坐标系中,有两条抛物线,它们的对称轴相同,则下列关系中,不正确的是( )| A. | m=k | B. | m=h | C. | k>n | D. | h<0,n>0 |
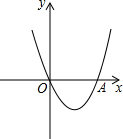 如图,已知抛物线的顶点在第四象限,顶点到x轴的距离为3,抛物线与x轴交于原点O(0,0)及点A,且OA=4.
如图,已知抛物线的顶点在第四象限,顶点到x轴的距离为3,抛物线与x轴交于原点O(0,0)及点A,且OA=4. 已知:如图,在?ABCD中,点E在BC边上,连接AE,O为AE中点,连接BO并延长交AD于F.
已知:如图,在?ABCD中,点E在BC边上,连接AE,O为AE中点,连接BO并延长交AD于F.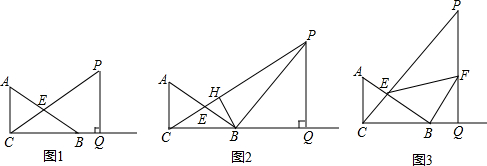
 如图,△ABC绕点O按逆时针方向旋转后,顶点A旋转到了点D.
如图,△ABC绕点O按逆时针方向旋转后,顶点A旋转到了点D.