题目内容
19.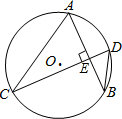 如图,AB、CD是⊙O弦,且AB⊥CD,若∠CDB=50°,则∠ACD的大小为( )
如图,AB、CD是⊙O弦,且AB⊥CD,若∠CDB=50°,则∠ACD的大小为( )| A. | 30° | B. | 35° | C. | 40° | D. | 50° |
分析 利用垂直的定义得到∠DPB=90°,再根据三角形内角和定理求出∠B=180°-90°-50°=40°,然后根据圆周角定理即可得到∠ACD的度数.
解答 解:∵AB⊥CD
∴∠DEB=90°,
∵∠CDB=50°,
∴∠B=180°-90°-50°=40°,
∴∠ACD=∠B=40°.
故选C.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.

练习册系列答案
相关题目
4. 如图,在平面直角坐标系中,有两条抛物线,它们的对称轴相同,则下列关系中,不正确的是( )
如图,在平面直角坐标系中,有两条抛物线,它们的对称轴相同,则下列关系中,不正确的是( )
 如图,在平面直角坐标系中,有两条抛物线,它们的对称轴相同,则下列关系中,不正确的是( )
如图,在平面直角坐标系中,有两条抛物线,它们的对称轴相同,则下列关系中,不正确的是( )| A. | m=k | B. | m=h | C. | k>n | D. | h<0,n>0 |
 已知:如图,在?ABCD中,点E在BC边上,连接AE,O为AE中点,连接BO并延长交AD于F.
已知:如图,在?ABCD中,点E在BC边上,连接AE,O为AE中点,连接BO并延长交AD于F.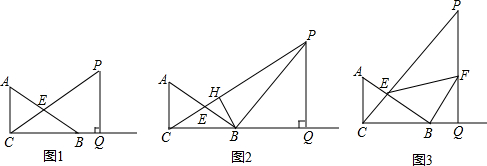
 如图,AD是⊙O的直径,弦BC⊥AD,连接AB、AC、OC,若∠COD=60°,则∠BAD=30°.
如图,AD是⊙O的直径,弦BC⊥AD,连接AB、AC、OC,若∠COD=60°,则∠BAD=30°. 如图,在一条笔直的小路上有一盏路灯,晚上小雷从点B处径直走到点A处时,小雷在灯光照射下的影长y与行走的路程x之间的函数图象大致是( )
如图,在一条笔直的小路上有一盏路灯,晚上小雷从点B处径直走到点A处时,小雷在灯光照射下的影长y与行走的路程x之间的函数图象大致是( )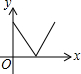
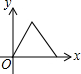
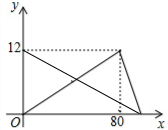 完全相同的甲、乙两个水槽,分别有一个进水管和若干个出水管,甲槽有12升水,由于工作人员马虎,他关闭进水管和出水管时,有一个出水管未关,水以每分钟0.12升的速度滴下,乙槽原来没有水,同时开放进水管和一个出水管一段时间后,关闭进水管,又打开a个出水管,存水量y(升)与时x(分)之间的函数图象如图所示,请结合图象回答问题:
完全相同的甲、乙两个水槽,分别有一个进水管和若干个出水管,甲槽有12升水,由于工作人员马虎,他关闭进水管和出水管时,有一个出水管未关,水以每分钟0.12升的速度滴下,乙槽原来没有水,同时开放进水管和一个出水管一段时间后,关闭进水管,又打开a个出水管,存水量y(升)与时x(分)之间的函数图象如图所示,请结合图象回答问题: