Question

20．如图，在笔直的公路L的同侧有A、B两个村庄，已知A、B两村分别到公路的距离AC=3km，BD=4km．现要在公路上建一个汽车站P，使该车站到A、B两村的距离相等，
（1）试用直尺和圆规在图中作出点P；（保留作图痕迹）
（2）若连接AP、BP，测得∠APB=90°，求A村到车站的距离．

Answer 1

分析 （1）连接AB，作AB的垂直平分线与AB交于点P即可；
（2）先利用AAS证明△ACP≌△PDB，得出CP=BD=4km，然后在Rt△ACP中利用勾股定理求出AP²=AC²+CP²=3²+4²=25，则AP=5．

解答 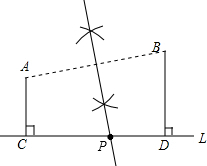解：（1）连结AB，画出AB的垂直平分线交CD于P，
则点P即为所求的点；

（2）∵∠APB=90°，
∴∠APC+∠BPD=90°，
又∵∠APC+∠CAP=90°，
∴∠CAP=∠BPD，
又∵∠ACP=∠PDB=90°，
∵MN垂直平分AB，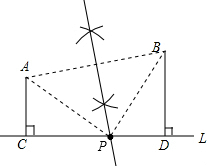
∴AP=BP，
∴△ACP≌△PDB（AAS），
∴CP=BD=4km，
在Rt△ACP中，∠ACP=90°，
AP²=AC²+CP²=3²+4²=25，
∴AP=5．
答：A村到车站的距离5km．

点评 本题考查了勾股定理的应用，线段垂直平分线的判定，全等三角形的判定与性质，作线段的垂直平分线，作出点P是解题的关键．