题目内容
5.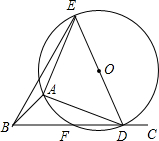 如图,∠ABC=45°,△ADE是等腰直角三角形,AE=AD,顶点A,D分别在∠ABC的两边BA,BC上滑动(不与点B重合),△ADE的外接圆交BC于点F,O为圆心.
如图,∠ABC=45°,△ADE是等腰直角三角形,AE=AD,顶点A,D分别在∠ABC的两边BA,BC上滑动(不与点B重合),△ADE的外接圆交BC于点F,O为圆心.(1)连接AF,EF,则∠AFE=45°;
(2)当点D在点F的右侧时,
①求证:EF=BD;
②若AB=4$\sqrt{2}$,8$\sqrt{2}$<BE≤4$\sqrt{13}$,则⊙O的面积S的取值范围是16π<S≤40π.
分析 (1)由$\widehat{AE}$=$\widehat{AE}$可知∠AFE=∠ADE=45°.
(2)①根据等腰直角三角形得∠ADE=45°,则∠ABD=∠AFE,再利用同弧所对的圆周角相等可知:∠AEF=∠ADB,根据AAS证明△ABD≌△AFE;
②由全等可知:BD=EF,∠EAF=∠BAD,因此设BD=x,则EF=x,根据等式的性质得∠BAF=∠EAD=90°,则△ABF是等腰直角三角形,计算得BF=8,则DF=x-8,根据勾股定理得BE2=EF2+BF2,求出x的取值为8<x≤12,同时由圆的面积公式计算得:S=$\frac{π}{2}$(x-4)2+8π,根据二次函数的增减性得出:16π<S≤40π.
解答 (1)解:如图,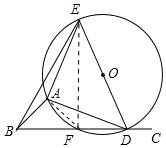 ∵AE=AD,∠EAD=90°,
∵AE=AD,∠EAD=90°,
∴∠ADE=∠AED=45°,
∵$\widehat{AE}$=$\widehat{AE}$,
∴∠AFE=∠ADE=45°,
故答案为45°.
(2)①证明:∵∠ADE=∠AFE=45°,∠ABD=45°,
∴∠ABD=∠AFE,
∵$\widehat{AF}$=$\widehat{AF}$,
∴∠AEF=∠ADB,
∵DE是直径,
∴∠EFD=∠EFB=90°,
∴∠AFB=∠B=45°,
∴AB=AF,
在△ABD和△AFE中,
$\left\{\begin{array}{l}{∠ADB=∠AEF}\\{∠B=∠AFE}\\{AB=AF}\end{array}\right.$
∴△ABD≌△AFE;
②解:∵△ABD≌△AFE,
∴BD=EF,∠EAF=∠BAD,
∴∠BAF=∠EAD=90°,
∵AB=4 $\sqrt{2}$,
∴BF=$\frac{AB}{cos∠ABF}$=$\frac{4\sqrt{2}}{\frac{\sqrt{2}}{2}}$=8,
设BD=x,则EF=x,DF=x-8,
∵BE2=EF2+BF2,8 $\sqrt{2}$<BE≤4 $\sqrt{13}$,
∴128<EF2+82≤208,
∴8<EF≤12,即8<x≤12,
则S=$\frac{π}{4}$DE2=$\frac{π}{4}$[x2+(x-8)2]=$\frac{π}{2}$(x-4)2+8π,
∵$\frac{π}{2}$>0,
∴抛物线的开口向上,
又∵对称轴为直线x=4,
∴当8<x≤12时,S随x的增大而增大,
∴16π<S≤40π.
故答案为16π<S≤40π.
点评 本题是圆的综合题、等腰直角三角形、三角函数、全等三角形的判定和性质、二次函数的性质、勾股定理等知识,解题的关键是灵活运用所学知识,学会构建二次函数利用二次函数的性质解决问题,属于中考压轴题.

 53随堂测系列答案
53随堂测系列答案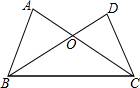 如图,下列条件中,不能证明△ABC≌△DCB的是( )
如图,下列条件中,不能证明△ABC≌△DCB的是( )| A. | AB=DC,AC=DB | B. | AB=DC,∠ABC=∠DCB | C. | AC=BD,∠A=∠D | D. | BO=CO,∠A=∠D |
| A. | (1,-3) | B. | (1,3) | C. | (-1,3) | D. | (-1,-3) |
| A. | -1 | B. | 0 | C. | 1 | D. | 0或1 |
| A. | $\frac{m}{12}$米 | B. | $\frac{ma}{12}$米 | C. | $\frac{ma}{6}$米 | D. | $\frac{ma}{3}$米 |
 已知,如图,CB∥OA,∠C=∠OAB=120°,E、F在CB上,且满足∠FOB=∠FBO,OE平分∠COF,
已知,如图,CB∥OA,∠C=∠OAB=120°,E、F在CB上,且满足∠FOB=∠FBO,OE平分∠COF, 如图所示,等边三角形ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,求CD的长.
如图所示,等边三角形ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,求CD的长.