题目内容
15. 已知,如图,CB∥OA,∠C=∠OAB=120°,E、F在CB上,且满足∠FOB=∠FBO,OE平分∠COF,
已知,如图,CB∥OA,∠C=∠OAB=120°,E、F在CB上,且满足∠FOB=∠FBO,OE平分∠COF,(1)求∠EOB的度数
(2)若向右平行移动AB,其他条件不变,那么∠OBC:∠OFC的值是否发生变化?若变化,找出其中的规律,若不变,求出这个比值
(3)若向右平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,请直接写出∠OBA的度数,若不存在,说明理由.
分析 (1)根据两直线平行,同旁内角互补求出∠AOC,然后求出∠EOB=$\frac{1}{2}$∠AOC,计算即可得解;
(2)根据两直线平行,内错角相等可得∠AOB=∠OBC,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠OFC=2∠OBC,从而得解;
(3)根据三角形的内角和定理求出∠COE=∠AOB,从而得到OB、OE、OF是∠AOC的四等分线,再利用三角形的内角和定理列式计算即可得解.
解答 解:(1)∵CB∥OA,
∴∠AOC=180°-∠C=180°-120°=60°,
∵OE平分∠COF,
∴∠COE=∠EOF,
∵∠FOB=∠AOB,
∴∠EOB=∠EOF+∠FOB=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×60°=30°;
(2)∵CB∥OA,
∴∠AOB=∠OBC,
∵∠FOB=∠AOB,
∴∠FOB=∠OBC,
∴∠OFC=∠FOB+∠OBC=2∠OBC,
∴∠OBC:∠OFC=1:2,是定值;
(3)在△COE和△AOB中,
∵∠OEC=∠OBA,∠C=∠OAB,
∴∠COE=∠AOB,
∴OB、OE、OF是∠AOC的四等分线,
∴∠COE=$\frac{1}{4}$∠AOC=$\frac{1}{4}$×60°=15°,
∴∠OEC=180°-∠C-∠COE=180°-120°-15°=45°,
故存在某种情况,使∠OEC=∠OBA,此时∠OEC=∠OBA=45°.
点评 本题考查了平行线的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,熟记各性质并准确识图理清图中各角度之间的关系是解题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
5.下面分解因式中正确的是( )
| A. | -a2+b2=-(b+a)(b-a) | B. | a2-b2-1=(a+b)(a-b)-1 | ||
| C. | (a+1)2-(y-1)2=(a+y)(a-y+2) | D. | m4-81=(m2+9)(m2-9) |
20.若a≤-2,化简$\sqrt{(a-2)^{2}}$+|3-a|的正确结果是( )
| A. | -1 | B. | 5 | C. | 2a-5 | D. | 5-2a |
4.下列说法中,正确的是( )
| A. | 一个有理数不是正有理数就是负有理数 | |
| B. | 0是整数但不是正数 | |
| C. | 非正数是指负整数和负分数 | |
| D. | 一个整数不是正整数就是负整数 |
 如图,AB∥CD,请你添加一个条件BE∥CF,使∠ABE=∠DCF.
如图,AB∥CD,请你添加一个条件BE∥CF,使∠ABE=∠DCF.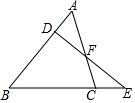 如图,已知△ABC的边AB上有一点D,边BC的延长线上有一点E,且AD=CE.DE交AC于点F,试证明:AB•DF=BC•EF.
如图,已知△ABC的边AB上有一点D,边BC的延长线上有一点E,且AD=CE.DE交AC于点F,试证明:AB•DF=BC•EF.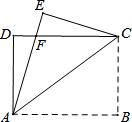 如图,矩形纸片ABCD中,AB=8cm,把矩形纸片沿线AC折叠,点B落在点E处,AE交DC于点F,若AD=$\frac{3}{2}$cm,则AF的长为$\frac{265}{64}$.
如图,矩形纸片ABCD中,AB=8cm,把矩形纸片沿线AC折叠,点B落在点E处,AE交DC于点F,若AD=$\frac{3}{2}$cm,则AF的长为$\frac{265}{64}$.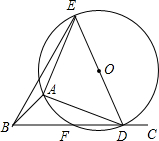 如图,∠ABC=45°,△ADE是等腰直角三角形,AE=AD,顶点A,D分别在∠ABC的两边BA,BC上滑动(不与点B重合),△ADE的外接圆交BC于点F,O为圆心.
如图,∠ABC=45°,△ADE是等腰直角三角形,AE=AD,顶点A,D分别在∠ABC的两边BA,BC上滑动(不与点B重合),△ADE的外接圆交BC于点F,O为圆心.