题目内容
按一定次序排列的一列数中任意三个相邻数之和都是24,已知第2个数为15,第4个数比第6个数小3,则第100个数为 .
考点:规律型:数字的变化类
专题:规律型
分析:根据任意三个相邻的数的和相等判断出每3个数为一组依次循环,从而得到第3个数与第6个数相等,设第3个数为x,表示出第4个数,然后列出方程求出第3、4两个数,再用100除以3求出第100个数所在的组数和这一组的序数,然后解答即可.
解答:解:∵任意三个相邻数之和都是24,
∴第3个数与第6个数相等,
设第3个数为x,则第6个数为x,
∵第4个数比第6个数小3,
∴第4个数为x-3,
∴15+x+(x-3)=24,
解得x=6,
∴第4个数6-3=3,
∵100÷3=33余1,
∴第100个数为第34循环组的第1个数,与第4个数相等,
∴第100个数为3.
故答案为:3.
∴第3个数与第6个数相等,
设第3个数为x,则第6个数为x,
∵第4个数比第6个数小3,
∴第4个数为x-3,
∴15+x+(x-3)=24,
解得x=6,
∴第4个数6-3=3,
∵100÷3=33余1,
∴第100个数为第34循环组的第1个数,与第4个数相等,
∴第100个数为3.
故答案为:3.
点评:本题是对数字变化规律的考查,读懂题目信息,判断出每3个数为一组依次循环是解题的关键.

练习册系列答案
相关题目
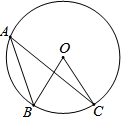 如图,点A、B、C在⊙O上,∠B=52°,∠C=18°,则∠A的度数为( )
如图,点A、B、C在⊙O上,∠B=52°,∠C=18°,则∠A的度数为( )| A、30° | B、20° |
| C、34° | D、28° |
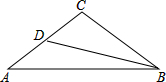 如图,△ABC中,CA=CB,∠ACB=108°,BD平分∠ABC交AC于D,求证:AB=AD+BC.
如图,△ABC中,CA=CB,∠ACB=108°,BD平分∠ABC交AC于D,求证:AB=AD+BC.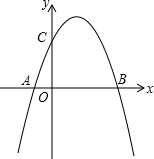 如图,抛物线y=ax2-3ax+b与x轴交于A和B(4,0),与y轴交于C点,并且OB=OC,点P为抛物线上一点.
如图,抛物线y=ax2-3ax+b与x轴交于A和B(4,0),与y轴交于C点,并且OB=OC,点P为抛物线上一点.



