题目内容
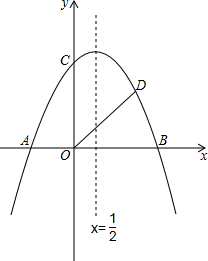
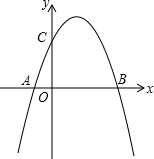 如图,抛物线y=ax2-3ax+b与x轴交于A和B(4,0),与y轴交于C点,并且OB=OC,点P为抛物线上一点.
如图,抛物线y=ax2-3ax+b与x轴交于A和B(4,0),与y轴交于C点,并且OB=OC,点P为抛物线上一点.(1)求抛物线的解析式;
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P 的坐标;若不存在,说明理由;
(3)若P为抛物线上位于第二象限上的一点,PH⊥x轴于H,交AC于Q点,当线段PQ最长时,求PQ:QH.
考点:二次函数综合题
专题:压轴题
分析:(1)根据OB=OC写出点C的坐标,然后代入抛物线求出a、b的值,即可得解;
(2)求出线段AC绕点A顺时针旋转90°后的对应点C′、绕点C逆时针旋转90°后的对应点A′的坐标,然后利用待定系数法求出直线AC′、CA′的解析式,再分别与抛物线解析式联立求解即可;
(3)求出直线AC的解析式,然后表示出PQ,再根据二次函数的最值问题求出PQ的最大值,然后求出QH,再相比计算即可得解.
(2)求出线段AC绕点A顺时针旋转90°后的对应点C′、绕点C逆时针旋转90°后的对应点A′的坐标,然后利用待定系数法求出直线AC′、CA′的解析式,再分别与抛物线解析式联立求解即可;
(3)求出直线AC的解析式,然后表示出PQ,再根据二次函数的最值问题求出PQ的最大值,然后求出QH,再相比计算即可得解.
解答:解:(1)∵OB=OC,B(4,0),
∴点C的坐标为(0,4),
将点B(4,0),C(0,4)代入抛物线y=ax2-3ax+b得,
,
解得
,
∴抛物线解析式为y=-x2+3x+4;
(2)令y=0,则-x2+3x+4=0,
解得x1=-1,x2=4,
所以,点A的坐标为(-1,0),
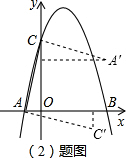
如图,①线段AC绕点A顺时针旋转90°后的对应点C′(3,-1),
设直线AC′的解析式为y=kx+b,
则
,
解得
,
所以,直线AC′的解析式为y=-
x-
,
联立
,
解得
,
,
所以,点P的坐标为(
,-
),
②线段AC绕点C逆时针旋转90°后的对应点A′的坐标为(4,3),
设直线CA′的解析式为y=mx+n,
则
,
解得
,
所以,直线CA′的解析式为y=-
x+4,
联立
,
解得
,
,
所以,点P的坐标为(
,
),
综上所述,点P(
,-
)或(
,
)时,△ACP是以AC为直角边的直角三角形;
(3)设直线AC的解析式为y=ex+f,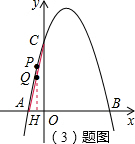
将A(-1,0),C(0,4)代入得,
,
解得
,
所以,直线AC的解析式为y=4x+4,
∵PH⊥x轴于H,
∴PQ=(-x2+3x+4)-(4x+4)=-x2-x=-(x+
)2+
,
∴当x=-
时,PQ有最大值
,
此时,QH=4×(-
)+4=-2+4=2,
∴PQ:QH=
:2=1:8.
∴点C的坐标为(0,4),
将点B(4,0),C(0,4)代入抛物线y=ax2-3ax+b得,
|
解得
|
∴抛物线解析式为y=-x2+3x+4;
(2)令y=0,则-x2+3x+4=0,
解得x1=-1,x2=4,
所以,点A的坐标为(-1,0),
如图,①线段AC绕点A顺时针旋转90°后的对应点C′(3,-1),
设直线AC′的解析式为y=kx+b,
则
|
解得
|
所以,直线AC′的解析式为y=-
| 1 |
| 4 |
| 1 |
| 4 |
联立
|

解得
|
|
所以,点P的坐标为(
| 17 |
| 4 |
| 21 |
| 16 |
②线段AC绕点C逆时针旋转90°后的对应点A′的坐标为(4,3),
设直线CA′的解析式为y=mx+n,
则
|
解得
|
所以,直线CA′的解析式为y=-
| 1 |
| 4 |
联立
|
解得
|
|
所以,点P的坐标为(
| 13 |
| 4 |
| 51 |
| 16 |
综上所述,点P(
| 17 |
| 4 |
| 21 |
| 16 |
| 13 |
| 4 |
| 51 |
| 16 |
(3)设直线AC的解析式为y=ex+f,

将A(-1,0),C(0,4)代入得,
|
解得
|
所以,直线AC的解析式为y=4x+4,
∵PH⊥x轴于H,
∴PQ=(-x2+3x+4)-(4x+4)=-x2-x=-(x+
| 1 |
| 2 |
| 1 |
| 4 |
∴当x=-
| 1 |
| 2 |
| 1 |
| 4 |
此时,QH=4×(-
| 1 |
| 2 |
∴PQ:QH=
| 1 |
| 4 |
点评:本题是二次函数综合题型,主要利用了待定系数法求二次函数解析式,待定系数法求一次函数解析式,二次函数的最值问题,难点在于(2)求出另一直角边所在的直线的解析式,(3)列式得到PQ的长度表达式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
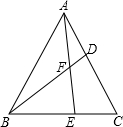 已知△ABC是等边三角形,点D、E分别在AC、BC边上,且AD=CE,AE与BD交于点F,则∠AFD的度数为( )
已知△ABC是等边三角形,点D、E分别在AC、BC边上,且AD=CE,AE与BD交于点F,则∠AFD的度数为( )| A、60° | B、45° |
| C、75° | D、70° |
如图,数轴的画法正确的是( )
A、 |
B、 |
C、 |
D、 |
 如图,抛物线y=-
如图,抛物线y=-
 用小立方体搭一个几何体,使它从正面、从上面看到的形状图如图所示,这样的几何体只有一种吗?它最多需要多少个小立方体?它最少需要多少个小立方体?请你画出这两种情况下的从左面看到的形状图.
用小立方体搭一个几何体,使它从正面、从上面看到的形状图如图所示,这样的几何体只有一种吗?它最多需要多少个小立方体?它最少需要多少个小立方体?请你画出这两种情况下的从左面看到的形状图.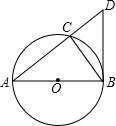 如图:⊙O是△ABC的外接圆,圆心O在AB上,过点B作⊙O的切线交AC的延长线于点D.
如图:⊙O是△ABC的外接圆,圆心O在AB上,过点B作⊙O的切线交AC的延长线于点D. 已知,△ABC中,AD⊥BC于点D,DF⊥AC于点F,DE⊥AB于点E,DF=DE,求证:AB=AC.
已知,△ABC中,AD⊥BC于点D,DF⊥AC于点F,DE⊥AB于点E,DF=DE,求证:AB=AC.