题目内容
在△ABC中，AB=6cm，AC=13cm，则BC边上的中线的取值范围是 ．
考点：全等三角形的判定与性质,三角形三边关系
专题：
分析：延长AD到E，使AD=DE，连接CE，则可得△ABD≌△ECD，得出AB=CE，在△ACE中，由三角形三边关系，即可求解结论．
解答：
解：延长AD到E，使AD=DE，连接CE，如图，
∵AD是△ABC中BC边上的中线，
∴BD=CD，
在△ABD和△ECD中，
，
∴△ABD≌△ECD（SAS），
∴AB=CE，
在△ACE中，AC-CE＜AE＜AC+CE，即AC-AB＜AE＜AC+AB，
13-6＜AE＜13+6，即7＜AE＜19，
∴3.5＜AD＜9.5，
故答案为：大于3.5且小于9.5．
解：延长AD到E，使AD=DE，连接CE，如图，∵AD是△ABC中BC边上的中线，
∴BD=CD，
在△ABD和△ECD中，
|
∴△ABD≌△ECD（SAS），
∴AB=CE，
在△ACE中，AC-CE＜AE＜AC+CE，即AC-AB＜AE＜AC+AB，
13-6＜AE＜13+6，即7＜AE＜19，
∴3.5＜AD＜9.5，
故答案为：大于3.5且小于9.5．
点评：本题主要考查了全等三角形的判定及性质以及三角形三边关系问题，能够熟练运用是解此题的关键．
练习册系列答案
相关题目
小明不小心把三角形的玻璃摔碎成3块，现在要去玻璃店配一块完全一样的玻璃，他最省事的是带（ ）去．| A、① | B、② | C、③ | D、①和③ |
如图，已知：AB=AD，BC=DE，AC=AE，∠1=42°，求∠3的度数．
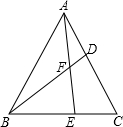已知△ABC是等边三角形，点D、E分别在AC、BC边上，且AD=CE，AE与BD交于点F，则∠AFD的度数为（ ）| A、60° | B、45° |
| C、75° | D、70° |
如图，在等腰Rt△ABC中，∠B=90°．将△ABC绕点A逆时针旋转60°得△AB′C′，则∠AB′C=