题目内容
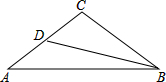 如图,△ABC中,CA=CB,∠ACB=108°,BD平分∠ABC交AC于D,求证:AB=AD+BC.
如图,△ABC中,CA=CB,∠ACB=108°,BD平分∠ABC交AC于D,求证:AB=AD+BC.考点:全等三角形的判定与性质
专题:证明题
分析:证明线段的和差倍分问题常用截长补短的方法.在线段AB上截取BE=BC,连接DE.则只需证明AD=AE即可.结合角度证明∠ADE=∠AED.
解答:证明:在线段BA上截取BE=BC,连接DE.
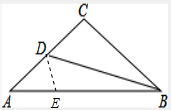
∵BD平分∠ABC,
∴∠ABD=∠EBD=
∠ABC.
在△CBD和△EBD中,
,
∴△CBD≌△EBD(SAS),
∴∠BED=∠ACB=108°,∠CDB=∠EDB.
又∵AB=AC,∠ACB=108°,∠CAB=∠ABC=
×(180°-108°)=36°,
∴∠CBD=∠EBD=18°.
∴∠CDB=∠EDB=180°-18°-108°=54°.
∴∠ADE=180°-∠CDB-∠EDB=180°-54°-54°=72°.
∴∠DEA=180°-∠DEB=180°-108°=72°.
∴∠ADE=∠AED.
∴AD=AE.
∴AB=BE+EA=CB+AD.

∵BD平分∠ABC,
∴∠ABD=∠EBD=
| 1 |
| 2 |
在△CBD和△EBD中,
|
∴△CBD≌△EBD(SAS),
∴∠BED=∠ACB=108°,∠CDB=∠EDB.
又∵AB=AC,∠ACB=108°,∠CAB=∠ABC=
| 1 |
| 2 |
∴∠CBD=∠EBD=18°.
∴∠CDB=∠EDB=180°-18°-108°=54°.
∴∠ADE=180°-∠CDB-∠EDB=180°-54°-54°=72°.
∴∠DEA=180°-∠DEB=180°-108°=72°.
∴∠ADE=∠AED.
∴AD=AE.
∴AB=BE+EA=CB+AD.
点评:此题考查全等三角形的判定和性质及等腰三角形的判定,综合性较强.

练习册系列答案
相关题目
下列各数中,无理数为( )
| A、0.15 | ||
| B、-4 | ||
| C、-π | ||
D、
|
 小明不小心把三角形的玻璃摔碎成3块,现在要去玻璃店配一块完全一样的玻璃,他最省事的是带( )去.
小明不小心把三角形的玻璃摔碎成3块,现在要去玻璃店配一块完全一样的玻璃,他最省事的是带( )去.| A、① | B、② | C、③ | D、①和③ |
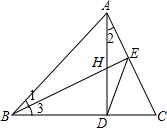 如图,在△ABC 中,高AD和高BE交于H点,且∠1=∠2=22.5°,下列结论中:①∠2=∠3;②BD=AD;③BD+DH=AB,其中结论正确的是( )
如图,在△ABC 中,高AD和高BE交于H点,且∠1=∠2=22.5°,下列结论中:①∠2=∠3;②BD=AD;③BD+DH=AB,其中结论正确的是( )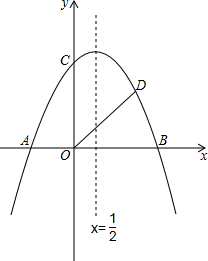 如图,抛物线y=-
如图,抛物线y=-
 如图,已知:AB=AD,BC=DE,AC=AE,∠1=42°,求∠3的度数.
如图,已知:AB=AD,BC=DE,AC=AE,∠1=42°,求∠3的度数.