题目内容
6.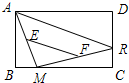 如图,矩形ABCD中,点R沿CD边从点C向点D运动,点M在BC边上运动,E、F分别是AM、MR的中点,则EF的长度随着点M、点R的运动( )
如图,矩形ABCD中,点R沿CD边从点C向点D运动,点M在BC边上运动,E、F分别是AM、MR的中点,则EF的长度随着点M、点R的运动( )| A. | 变短 | B. | 变长 | C. | 不变 | D. | 无法确定 |
分析 易得EF为三角形AMR的中位线,那么EF长恒等于定值AR的一半,进而分析得出答案.
解答 解:∵E,F分别是AM,MR的中点,
∴EF=$\frac{1}{2}$AR,
∵点R沿CD边从点C向点D运动,∴AR不断减小,
∴EF的长度随着点M、点R的运动而变短,
故选:A.
点评 本题考查了矩形的性质以及三角形中位线定理,正确把握三角形中位线等于第三边的一半的性质是解题关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
5.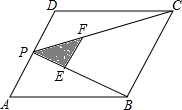 如图,P为平行四边形ABCD边AD上一点,E、F分别是PB、PC(靠近点P)的三等分点,△PEF、△PDC、△PAB的面积分别为S1、S2、S3,若AD=2,AB=2$\sqrt{3}$,∠A=60°,则S1+S2+S3的值为( )
如图,P为平行四边形ABCD边AD上一点,E、F分别是PB、PC(靠近点P)的三等分点,△PEF、△PDC、△PAB的面积分别为S1、S2、S3,若AD=2,AB=2$\sqrt{3}$,∠A=60°,则S1+S2+S3的值为( )
 如图,P为平行四边形ABCD边AD上一点,E、F分别是PB、PC(靠近点P)的三等分点,△PEF、△PDC、△PAB的面积分别为S1、S2、S3,若AD=2,AB=2$\sqrt{3}$,∠A=60°,则S1+S2+S3的值为( )
如图,P为平行四边形ABCD边AD上一点,E、F分别是PB、PC(靠近点P)的三等分点,△PEF、△PDC、△PAB的面积分别为S1、S2、S3,若AD=2,AB=2$\sqrt{3}$,∠A=60°,则S1+S2+S3的值为( )| A. | $\frac{10}{3}$ | B. | $\frac{9}{2}$ | C. | $\frac{13}{3}$ | D. | 4 |
6.下列图案中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
3.在平面直角坐标系中,点(-4,3)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
18.下列算式中,其中正确的有( )
①${({-\frac{1}{2}})^{-3}}=-\frac{1}{8}$,②a2+2a-1=(a-1)2,③a8÷a8=1(a≠0),④(a-b)2=a2-b2.
①${({-\frac{1}{2}})^{-3}}=-\frac{1}{8}$,②a2+2a-1=(a-1)2,③a8÷a8=1(a≠0),④(a-b)2=a2-b2.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.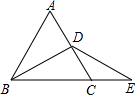 如图,在等边三角形ABC中,D是AC边上的中点,延长BC到点E,使CE=CD,则∠E的度数为( )
如图,在等边三角形ABC中,D是AC边上的中点,延长BC到点E,使CE=CD,则∠E的度数为( )
 如图,在等边三角形ABC中,D是AC边上的中点,延长BC到点E,使CE=CD,则∠E的度数为( )
如图,在等边三角形ABC中,D是AC边上的中点,延长BC到点E,使CE=CD,则∠E的度数为( )| A. | 15° | B. | 20° | C. | 30° | D. | 40° |
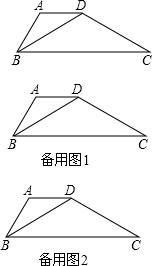 如图,在梯形纸片ABCD中,AD∥BC,AD=AB=4,BD=CD,∠C=30°,E为BC边上一点,以BE为直角边,E为直角顶点作等腰Rt△BEF,使等腰Rt△BEF和梯形ABCD在BC的同侧.
如图,在梯形纸片ABCD中,AD∥BC,AD=AB=4,BD=CD,∠C=30°,E为BC边上一点,以BE为直角边,E为直角顶点作等腰Rt△BEF,使等腰Rt△BEF和梯形ABCD在BC的同侧.