题目内容
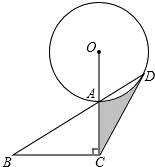 如图,已知在Rt△ABC中,∠B=30°,∠ACB=90°,延长CA到O,使AO=AC,以O为圆心,OA长为半径作⊙O交BA延长线于点D,连接CD.
如图,已知在Rt△ABC中,∠B=30°,∠ACB=90°,延长CA到O,使AO=AC,以O为圆心,OA长为半径作⊙O交BA延长线于点D,连接CD.(1)求证:CD是⊙O的切线;
(2)若AB=4,求图中阴影部分的面积.
考点:切线的判定,等边三角形的判定与性质,含30度角的直角三角形,勾股定理,扇形面积的计算
专题:计算题,证明题
分析:(1)连接OD,求出∠OAD=60°,得出等边三角形OAD,求出AD=OA=AC,∠ODA=∠O=60°,求出∠ADC=∠ACD=
∠OAD=30°,求出∠ODC=90°,根据切线的判定得出即可;
(2)求出OD,根据勾股定理求出CD长,分别求出三角形ODC和扇形AOD的面积,相减即可.
| 1 |
| 2 |
(2)求出OD,根据勾股定理求出CD长,分别求出三角形ODC和扇形AOD的面积,相减即可.
解答: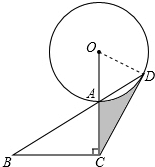 (1)证明:连接OD,
(1)证明:连接OD,
∵∠BCA=90°,∠B=30°,
∴∠OAD=∠BAC=60°,
∵OD=OA,
∴△OAD是等边三角形,
∴AD=OA=AC,∠ODA=∠O=60°,
∴∠ADC=∠ACD=
∠OAD=30°,
∴∠ODC=60°+30°=90°,
即OD⊥DC,
∵OD为半径,
∴CD是⊙O的切线;
(2)解:∵AB=4,∠ACB=90°,∠B=30°,
∴OD=OA=AC=
AB=2,
由勾股定理得:CD=
=
=2
,
∴S阴影=S△ODC-S扇形AOD=
×2×2
-
=2
-
π.
 (1)证明:连接OD,
(1)证明:连接OD,∵∠BCA=90°,∠B=30°,
∴∠OAD=∠BAC=60°,
∵OD=OA,
∴△OAD是等边三角形,
∴AD=OA=AC,∠ODA=∠O=60°,
∴∠ADC=∠ACD=
| 1 |
| 2 |
∴∠ODC=60°+30°=90°,
即OD⊥DC,
∵OD为半径,
∴CD是⊙O的切线;
(2)解:∵AB=4,∠ACB=90°,∠B=30°,
∴OD=OA=AC=
| 1 |
| 2 |
由勾股定理得:CD=
| OC2-OD2 |
| 42-22 |
| 3 |
∴S阴影=S△ODC-S扇形AOD=
| 1 |
| 2 |
| 3 |
| 60π×22 |
| 360 |
| 3 |
| 2 |
| 3 |
点评:本题考查了扇形的面积,切线的判定,含30度角的直角三角形的性质,勾股定理,等边三角形的性质和判定的应用,主要考查学生综合运用性质进行推理和计算的能力,综合性比较强,有一定的难度.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
若a+
b+2c=0,则关于x的方程ax2-bx+c=0(a≠0,且a≠2c)的根的情况是( )
| 2 |
| A、没有实数根 |
| B、有两个相等的实数根 |
| C、有两个不相等的实数根 |
| D、无法判断 |
 如图,在矩形ABCD中,AB=4,BC=3,点O为对角线BD的中点,点P从点A出发,沿折线AD-DO-OC以每秒1个单位长度的速度向终点C运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与△ABD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
如图,在矩形ABCD中,AB=4,BC=3,点O为对角线BD的中点,点P从点A出发,沿折线AD-DO-OC以每秒1个单位长度的速度向终点C运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与△ABD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).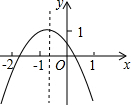 二次函数y=ax2+bx+c(a≠0)的图象如图,若M=a+b-c,N=4a-2b+c,P=2a-b,Q=b2-4ac.则M,N,P,Q中,值小于0的数有
二次函数y=ax2+bx+c(a≠0)的图象如图,若M=a+b-c,N=4a-2b+c,P=2a-b,Q=b2-4ac.则M,N,P,Q中,值小于0的数有