题目内容
若a+
b+2c=0,则关于x的方程ax2-bx+c=0(a≠0,且a≠2c)的根的情况是( )
| 2 |
| A、没有实数根 |
| B、有两个相等的实数根 |
| C、有两个不相等的实数根 |
| D、无法判断 |
考点:根的判别式
专题:
分析:先根据题意求得b=-
=-
,再根据根的判别式△和0的大小关系,得出答案.
| a+2c | ||
|
| ||
| 2 |
解答:解:∵△=b2-4ac=
(a+2c)2-4ac
=
(a2+4c2)+2ac-4ac
=
(a2+4c2)-2ac
=(a-2c)2,
∵a≠2c,
∴a-2c≠0,
∴(a-2c)2>0,
∴关于x的方程ax2-bx+c=0有两个不相等的实数根,
故选C.
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=(a-2c)2,
∵a≠2c,
∴a-2c≠0,
∴(a-2c)2>0,
∴关于x的方程ax2-bx+c=0有两个不相等的实数根,
故选C.
点评:本题考查了根的判别式以及非负数的性质,是中考常见的题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知n是方程x2-2x-1=0的一个根,则3n2-6n-7的值为( )
| A、-5 | B、-4 | C、-3 | D、-2 |
将5.62×10-4用小数表示为( )
| A、0.000 562 |
| B、0.000 056 2 |
| C、0.005 62 |
| D、0.000 005 62 |
2的相反数是( )
| A、2 | ||
| B、-2 | ||
C、-
| ||
D、
|
下列计算正确的是( )
| A、a2+a2=a4 |
| B、3-1=-3 |
| C、x6÷x2=x4 |
| D、(a3)2=a5 |
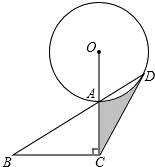 如图,已知在Rt△ABC中,∠B=30°,∠ACB=90°,延长CA到O,使AO=AC,以O为圆心,OA长为半径作⊙O交BA延长线于点D,连接CD.
如图,已知在Rt△ABC中,∠B=30°,∠ACB=90°,延长CA到O,使AO=AC,以O为圆心,OA长为半径作⊙O交BA延长线于点D,连接CD.