题目内容
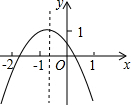 二次函数y=ax2+bx+c(a≠0)的图象如图,若M=a+b-c,N=4a-2b+c,P=2a-b,Q=b2-4ac.则M,N,P,Q中,值小于0的数有
二次函数y=ax2+bx+c(a≠0)的图象如图,若M=a+b-c,N=4a-2b+c,P=2a-b,Q=b2-4ac.则M,N,P,Q中,值小于0的数有考点:二次函数图象与系数的关系
专题:
分析:先判断出a、b、c的符号即可得M=a+b-c<0;根据当x=-2时,y=4a-2b+c<0,可判断N=4a-2b+c<0;由对称轴与-1的关系,可判断P=2a-b<0;根据
图象与x轴的交点个数,可得Q=b2-4ac>0.所以值小于0的数有3个.
图象与x轴的交点个数,可得Q=b2-4ac>0.所以值小于0的数有3个.
解答:解:∵图象开口向下,
∴a<0,
∵对称轴在y轴左侧,
∴a,b同号,∴a<0,b<0,
∵图象经过y轴正半轴,∴c>0,
∴M=a+b-c<0;
当x=-2时,y=4a-2b+c<0,∴N=4a-2b+c<0;
∵-
>-1,
∵a<0,
∴b>2a,
∴2a-b<0,
∴P=2a-b<0;
∵图象与x轴有两个交点,
∴b2-4ac>0,Q=b2-4ac>0.
值小于0的数有M,N,P共3个.
故答案为:3.
∴a<0,
∵对称轴在y轴左侧,
∴a,b同号,∴a<0,b<0,
∵图象经过y轴正半轴,∴c>0,
∴M=a+b-c<0;
当x=-2时,y=4a-2b+c<0,∴N=4a-2b+c<0;
∵-
| b |
| 2a |
∵a<0,
∴b>2a,
∴2a-b<0,
∴P=2a-b<0;
∵图象与x轴有两个交点,
∴b2-4ac>0,Q=b2-4ac>0.
值小于0的数有M,N,P共3个.
故答案为:3.
点评:本题主要考查了图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
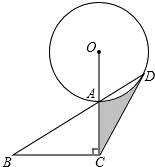 如图,已知在Rt△ABC中,∠B=30°,∠ACB=90°,延长CA到O,使AO=AC,以O为圆心,OA长为半径作⊙O交BA延长线于点D,连接CD.
如图,已知在Rt△ABC中,∠B=30°,∠ACB=90°,延长CA到O,使AO=AC,以O为圆心,OA长为半径作⊙O交BA延长线于点D,连接CD. 如图,当太阳在A处时,小明测得某树的影长为2米,当太阳在B处时又测得该树的影长为8米.若两次日照的光线互相垂直,则这颗树的高度为
如图,当太阳在A处时,小明测得某树的影长为2米,当太阳在B处时又测得该树的影长为8米.若两次日照的光线互相垂直,则这颗树的高度为 如图,从原点A开始,以AB=1为直径画半圆,记为第1个半圆;以BC=2为直径画半圆,记为第2个半圆;以CD=4为直径画半圆,记为第3个半圆;以DE=8为直径画半圆,记为第4个半圆;…,按此规律,继续画半圆,则第6个半圆的面积为
如图,从原点A开始,以AB=1为直径画半圆,记为第1个半圆;以BC=2为直径画半圆,记为第2个半圆;以CD=4为直径画半圆,记为第3个半圆;以DE=8为直径画半圆,记为第4个半圆;…,按此规律,继续画半圆,则第6个半圆的面积为 如图,已知∠1=∠2,∠B=∠C,试证明AB∥CD.
如图,已知∠1=∠2,∠B=∠C,试证明AB∥CD.