题目内容
6.若$\frac{3x-4}{(x-1)(x-2)}=\frac{A}{x-1}+\frac{B}{x-2}$,则B=2.分析 将$\frac{A}{x-1}$+$\frac{B}{x-2}$通分得到$\frac{A}{x-1}$+$\frac{B}{x-2}$=$\frac{(A+B)x-(2A+B)}{(x-1)(x-2)}$,再根据对应项相等得到关于A、B的方程组,解方程即可求解.
解答 解:∵$\frac{A}{x-1}$+$\frac{B}{x-2}$=$\frac{(A+B)x-(2A+B)}{(x-1)(x-2)}$,$\frac{3x-4}{(x-1)(x-2)}=\frac{A}{x-1}+\frac{B}{x-2}$,
∴$\left\{\begin{array}{l}{A+B=3}\\{2A+B=4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{A=1}\\{B=2}\end{array}\right.$.
故答案为:2.
点评 考查了分式的加减法,解题的关键是得到关于A、B的方程组.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
14.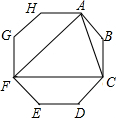 连接正八边形的三个顶点,得到如图所示的图形,下列说法错误的是( )
连接正八边形的三个顶点,得到如图所示的图形,下列说法错误的是( )
 连接正八边形的三个顶点,得到如图所示的图形,下列说法错误的是( )
连接正八边形的三个顶点,得到如图所示的图形,下列说法错误的是( )| A. | △ACF是等边三角形 | |
| B. | 连接BF,则BF分别平分∠AFC和∠ABC | |
| C. | 整个图形是轴对称图形,但不是中心对称图形 | |
| D. | 四边形AFGH与四边形CFED的面积相等 |
1.下列式子运算正确的是( )
| A. | 23=6 | B. | a2+a2=a5 | C. | a6÷a2=a4 | D. | 3a-2a=1 |
11.关于数据:25,26,23,27,26,23,20.下列说法正确的是( )
| A. | 中位数是27 | B. | 众数是23和26 | C. | 极差是6 | D. | 平均数是24.5 |
16.下列图案中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,已知AB是⊙O的弦,半径OA=2,OA和AB的长度是关于x的一元二次方程x2-4x+a=0的两个实数根.
如图,已知AB是⊙O的弦,半径OA=2,OA和AB的长度是关于x的一元二次方程x2-4x+a=0的两个实数根. 如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B.
如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B.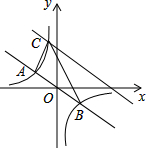 如图,在直角坐标系中,直线y=-$\frac{1}{2}$x与反比例函数y=$\frac{k}{x}$的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.
如图,在直角坐标系中,直线y=-$\frac{1}{2}$x与反比例函数y=$\frac{k}{x}$的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.