Question

1．有一弓行石桥，桥下的水面宽为2$\sqrt{21}$米，水面离弓顶的高度为3米，
（1）求弓形所在圆的半径．
（2）船一般的棚顶宽为4米，棚顶离水面的高度是2米，当水位上涨0.5米时，此船能通过吗？

Answer 1

分析 （1）首先连接OA，设这座拱桥所在圆的半径为x米，由垂径定理，易得方程：x²=（x-3）²+（$\sqrt{21}$）²，解此方程即可求得答案；
（2）连接OM，设MN=4米，可求得此时OH的高，即可求得OH-OD-0.5的长，比较2米，即可得到此时船能否顺利通过这座弓行石桥．

解答 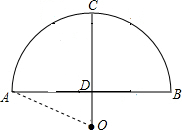解：（1）连接OA，
根据题意得：CD=3米，AB=2$\sqrt{21}$米，
则AD=$\frac{1}{2}$AB=$\sqrt{21}$（米），
设这座弓行石桥所在圆的半径为x米，
则OA=OC=x米，OD=OC-CD=（x-3）米，
在Rt△AOD中，OA²=OD²+AD²，
则x²=（x-3）²+（$\sqrt{21}$）²，
解得：x=5，
故这座弓行石桥所在圆的半径为5米．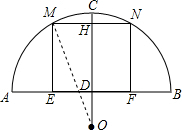

（2）货船能顺利通过这座弓行石桥．理由：
连接OM，
设MN=4米，
∵OC⊥MN，
∴MH=$\frac{1}{2}$MN=2（米），
在Rt△OMH中，OH=$\sqrt{O{M}^{2}-M{H}^{2}}$=$\sqrt{21}$（米），
∵OD=OC-CD=5-3=2（米）
∵OH-OD-0.5=$\sqrt{21}$-2.5＞2，
∴此船能顺利通过这座弓行石桥．

点评 此题考查了垂径定理的应用．此题难度适中，关键在于利用弧形所在的圆，构造出直角三角形，根据勾股定理进行求解计算．