题目内容
17.当a=-7时,关于x的方程$\frac{2ax+4}{a-x}$=$\frac{5}{4}$的解是1.分析 将x=1代入原方程,然后解关于a的分式方程即可.
解答 解:∵关于x的方程$\frac{2ax+4}{a-x}$=$\frac{5}{4}$的解是1.
即x=1,
将x=1代入原方程得:
$\frac{2a+4}{a-1}=\frac{5}{4}$,
解得:a=-7,
经检验,a=-7是$\frac{2a+4}{a-1}=\frac{5}{4}$的根,
∴方程$\frac{2a+4}{a-1}=\frac{5}{4}$的根为a=-7,
故答案为:-7.
点评 此题考查了分式方程的解,解题的关键是:解分式方程要验根.

练习册系列答案
相关题目
8.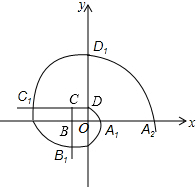 如图,边长为1正方形OBCD的顶点O在坐标原点,点B,D分别在x轴,y轴上,点C在第二象限,曲线DA1B1C1D1…叫做“正方形的渐开线”,其中$\widehat{D{A}_{1}}$,$\widehat{{A}_{1}{B}_{1}}$,$\widehat{{B}_{1}{C}_{1}}$,$\widehat{{C}_{1}{D}_{1}}$,…,的圆心依次按O,B,C,D循环,则点B5的坐标为( )
如图,边长为1正方形OBCD的顶点O在坐标原点,点B,D分别在x轴,y轴上,点C在第二象限,曲线DA1B1C1D1…叫做“正方形的渐开线”,其中$\widehat{D{A}_{1}}$,$\widehat{{A}_{1}{B}_{1}}$,$\widehat{{B}_{1}{C}_{1}}$,$\widehat{{C}_{1}{D}_{1}}$,…,的圆心依次按O,B,C,D循环,则点B5的坐标为( )
 如图,边长为1正方形OBCD的顶点O在坐标原点,点B,D分别在x轴,y轴上,点C在第二象限,曲线DA1B1C1D1…叫做“正方形的渐开线”,其中$\widehat{D{A}_{1}}$,$\widehat{{A}_{1}{B}_{1}}$,$\widehat{{B}_{1}{C}_{1}}$,$\widehat{{C}_{1}{D}_{1}}$,…,的圆心依次按O,B,C,D循环,则点B5的坐标为( )
如图,边长为1正方形OBCD的顶点O在坐标原点,点B,D分别在x轴,y轴上,点C在第二象限,曲线DA1B1C1D1…叫做“正方形的渐开线”,其中$\widehat{D{A}_{1}}$,$\widehat{{A}_{1}{B}_{1}}$,$\widehat{{B}_{1}{C}_{1}}$,$\widehat{{C}_{1}{D}_{1}}$,…,的圆心依次按O,B,C,D循环,则点B5的坐标为( )| A. | (-1,-5) | B. | (-1,-18) | C. | (-1,-14) | D. | (-18,-1) |
12.A、B两地相距80千米,一辆大汽车从A地开出2小时后,又从A地开出另一辆小汽车,已知小汽车的速度是大汽车速度的3倍,结果小汽车比大汽车早40分钟到达B地,求两种汽车每小时各走多少千米.设大汽车的速度为xkm/h,则下面所列方程正确的是( )
| A. | $\frac{80}{x}$-$\frac{80}{3x}$=40 | B. | $\frac{80}{x}$-$\frac{80}{3x}$=2.4 | C. | $\frac{80}{x}$-2=$\frac{80}{3x}$+$\frac{2}{3}$ | D. | $\frac{80}{x}$+2=$\frac{80}{3x}$-$\frac{2}{3}$ |
7. 如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则S△DEF:S△BCF=( )
如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则S△DEF:S△BCF=( )
 如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则S△DEF:S△BCF=( )
如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则S△DEF:S△BCF=( )| A. | 4:9 | B. | 1:4 | C. | 1:2 | D. | 1:1 |
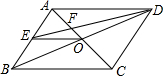 如图,O为?ABCD的对角线交点,E为AB的中点,DE交AC于点F,若S□ABCD=16,则S△DOE的值为2.
如图,O为?ABCD的对角线交点,E为AB的中点,DE交AC于点F,若S□ABCD=16,则S△DOE的值为2.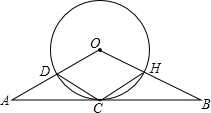 如图,等腰三角形AOB的一边BC经过⊙O上的一点C,AO=BO,CA=CB,OA与⊙O交于点D,OB与⊙O交于点H,连接CD、CH.
如图,等腰三角形AOB的一边BC经过⊙O上的一点C,AO=BO,CA=CB,OA与⊙O交于点D,OB与⊙O交于点H,连接CD、CH.
 已知AD为△ABC中BC边上的中线,CE∥AB交AD的延长线于E.
已知AD为△ABC中BC边上的中线,CE∥AB交AD的延长线于E.