题目内容
7. 如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则S△DEF:S△BCF=( )
如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则S△DEF:S△BCF=( )| A. | 4:9 | B. | 1:4 | C. | 1:2 | D. | 1:1 |
分析 根据题意得出△DEF∽△BCF,进而得出DE:BC=EF:FC,利用点E是边AD的中点得出其比值,再根据相似三角形的性质:面积比等于相似比的平方即可得问题答案.
解答 解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴△DEF∽△BCF,
∴DE:BC=EF:FC,
∵点E是边AD的中点,
∴AE=DE=$\frac{1}{2}$AD,
∴EF:FC=1:2,
∴S△DEF:S△BCF=1:4,
故选B.
点评 本题考查了平行四边形的性质以及相似三角形的判定和性质,解题的关键是掌握相似三角形的面积比等于相似比的平方.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.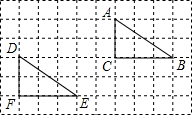 如图,在10×6的网格中,每个小方格的边长都是1个单位,将△DEF平移到△ABC的位置,下列平移方法正确的是( )
如图,在10×6的网格中,每个小方格的边长都是1个单位,将△DEF平移到△ABC的位置,下列平移方法正确的是( )
 如图,在10×6的网格中,每个小方格的边长都是1个单位,将△DEF平移到△ABC的位置,下列平移方法正确的是( )
如图,在10×6的网格中,每个小方格的边长都是1个单位,将△DEF平移到△ABC的位置,下列平移方法正确的是( )| A. | 先向左平移5个单位,再向下平移2个单位 | |
| B. | 先向右平移5个单位,再向下平移2个单位 | |
| C. | 先向左平移5个单位,再向上平移2个单位 | |
| D. | 先向右平移5个单位,再向上平移2个单位 |
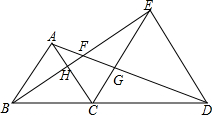 已知等边△ABC,等边△CDE,B、C、D共线.
已知等边△ABC,等边△CDE,B、C、D共线.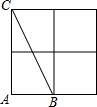 如图,△ABC的3个顶点分别在小正方形的顶点(格点)上,这样的三角形叫格点三角形,该图中与△ABC全等的不同格点三角形共有15个(△ABC除外).
如图,△ABC的3个顶点分别在小正方形的顶点(格点)上,这样的三角形叫格点三角形,该图中与△ABC全等的不同格点三角形共有15个(△ABC除外).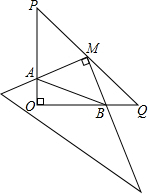 如图,在Rt△POQ中,OP=OQ=4,M是PQ中点,把一三角尺的直角顶点放在点M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.连结AB,在旋转三角尺的过程中,△AOB的周长的最小值4+2$\sqrt{2}$.
如图,在Rt△POQ中,OP=OQ=4,M是PQ中点,把一三角尺的直角顶点放在点M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.连结AB,在旋转三角尺的过程中,△AOB的周长的最小值4+2$\sqrt{2}$.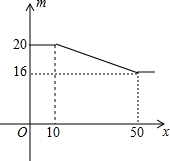 我市一家电子计算器专卖店的某种计算机每个进价13元,零售价20元,多买优惠;若顾客一次购买的数量x(个)与售出的单价m(元/个)的关系如图所示,售出的最低价为每个16元
我市一家电子计算器专卖店的某种计算机每个进价13元,零售价20元,多买优惠;若顾客一次购买的数量x(个)与售出的单价m(元/个)的关系如图所示,售出的最低价为每个16元 如图,直线l1、l2、…l6是一组等距的平行线,过直线l1上的点A作两条射线,分别与直线l3、l6相交于点B、E、C、F.若BC=2,则EF的长是5.
如图,直线l1、l2、…l6是一组等距的平行线,过直线l1上的点A作两条射线,分别与直线l3、l6相交于点B、E、C、F.若BC=2,则EF的长是5.