题目内容
8.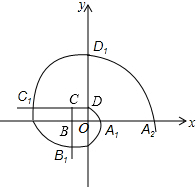 如图,边长为1正方形OBCD的顶点O在坐标原点,点B,D分别在x轴,y轴上,点C在第二象限,曲线DA1B1C1D1…叫做“正方形的渐开线”,其中$\widehat{D{A}_{1}}$,$\widehat{{A}_{1}{B}_{1}}$,$\widehat{{B}_{1}{C}_{1}}$,$\widehat{{C}_{1}{D}_{1}}$,…,的圆心依次按O,B,C,D循环,则点B5的坐标为( )
如图,边长为1正方形OBCD的顶点O在坐标原点,点B,D分别在x轴,y轴上,点C在第二象限,曲线DA1B1C1D1…叫做“正方形的渐开线”,其中$\widehat{D{A}_{1}}$,$\widehat{{A}_{1}{B}_{1}}$,$\widehat{{B}_{1}{C}_{1}}$,$\widehat{{C}_{1}{D}_{1}}$,…,的圆心依次按O,B,C,D循环,则点B5的坐标为( )| A. | (-1,-5) | B. | (-1,-18) | C. | (-1,-14) | D. | (-18,-1) |
分析 利用正方形的外角与n的关系,然后再利用渐开线中第n重的关系求值.
解答 解:若正方形的边长为1,
可得:点B1的坐标为(-1,)),点B2的坐标为(-1,-2),点B3的坐标为(-1,-6),点B4的坐标为(-1,-10),点B5的坐标为(-1,-14);
故选C
点评 此题考查点的坐标问题,本题的关键是明白正方形的外角与n的关系,然后再利用渐开线中第n重的关系求值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.下列长度的3条线段,能构成三角形的是( )
| A. | 1cm,4cm,3cm | B. | 2cm,3cm,4cm | C. | 4cm,4cm,8cm | D. | 5cm,6cm,12cm |
19.已知$\frac{a}{b}$=$\frac{3}{4}$,则$\frac{a+b}{b}$=( )
| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{7}{4}$ | D. | $\frac{4}{7}$ |
16.已知扇形AOB的圆心角∠AOB=120°,半径R=3cm,则与此扇形面积相等的圆的半径为( )
| A. | $\sqrt{2}$cm | B. | $\sqrt{3}$cm | C. | 3cm | D. | $\sqrt{5}$cm |
13.下列事件中是随机事件的是( )
| A. | 测量某天的最低气温,结果是-150℃ | |
| B. | 三角形内角和等于180° | |
| C. | 随意翻一本书的页码,这页的页码是奇数 | |
| D. | 通常加热到100℃时,水沸腾 |
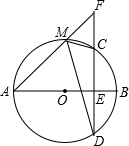 已知:如图,AB是⊙O的直径,CD为弦,且AB⊥CD于E,F为DC延长线上一点,连结AF交⊙O于M.
已知:如图,AB是⊙O的直径,CD为弦,且AB⊥CD于E,F为DC延长线上一点,连结AF交⊙O于M.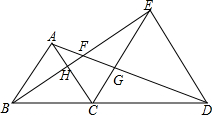 已知等边△ABC,等边△CDE,B、C、D共线.
已知等边△ABC,等边△CDE,B、C、D共线.