Question

10．平面直角坐标系中，点P（3，-2）关于点Q（1，0）成中心对称的点的坐标是（-1，2）．

Answer 1

分析 设Q（1，0），连结PQ并延长到点P′，使P′Q=PQ，设P′（x，y），则x＜0，y＞0．过P作PM⊥x轴于点M，过P′作PN⊥x轴于点N．利用AAS证明△QP′N≌△QPM，得出QN=QM，P′N=PM，即1-x=3-1，y=2，求出x=-1，y=2，进而得到P′的坐标．

解答 解：如图，设Q（1，0），连结PA并延长到点P′，使P′Q=PQ，设P′（x，y），则x＜0，y＞0．
过P作PM⊥x轴于点M，过P′作PN⊥x轴于点N．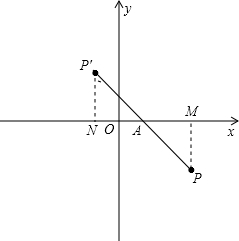
在△QP′N与△QPM中，
$\left\{\begin{array}{l}{∠QAP′=∠QMP}\\{∠NQP′=∠MQP}\\{QP′=QP}\end{array}\right.$，
∴△QP′N≌△QPM（AAS），
∴QN=QM，P′N=PM，
∴1-x=3-1，y=2，
∴x=-1，y=2，
∴P′（-1，2）．
故答案为（-1，2）．

点评 本题考查了坐标与图形变化-旋转，全等三角形的判定与性质，准确作出点P（3，-2）关于点（1，0）对称的点P′是解题的关键．