题目内容
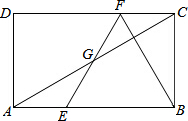 如图,在矩形ABCD中,E、F分别是AB、CD上的点,AE=CF,连接EF、BF,EF交对角线AC于点G,若BE=BF,∠DFE=2∠BAC,BC=2
如图,在矩形ABCD中,E、F分别是AB、CD上的点,AE=CF,连接EF、BF,EF交对角线AC于点G,若BE=BF,∠DFE=2∠BAC,BC=2| 3 |
考点:矩形的性质
专题:
分析:根据矩形的对边平行可得AB∥CD,再根据两直线平行,内错角相等可得∠GAE=∠GCF,然后利用“角角边”证明△AEG和△CFG全等,根据全等三角形对应边相等可得AG=CG,GE=GF,再根据等腰三角形三线合一的性质可得BG⊥EF,根据两直线平行,内错角相等可得∠DFE=∠BEF,根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BEF=∠BAC+∠AGE,然后求出∠BAC=∠AGE,根据等角对等边可得AE=GE,再求出CF=GF,然后利用“HL”证明Rt△BCF和Rt△BGF全等,根据全等三角形对应边相等可得BG=BC,再根据直角三角形斜边上的中线等于斜边的一半可得AC=2BG,然后利用勾股定理列式求出AB,最后利用三角形的面积公式列式计算即可得解.
解答:解:在矩形ABCD中,AB∥CD,
∴∠GAE=∠GCF,
在△AEG和△CFG中,
,
∴△AEG≌△CFG(AAS),
∴AG=CG,GE=GF,
∵BE=BF,
∴BG⊥EF(等腰三角形三线合一),
∵AB∥CD,
∴∠DFE=∠BEF,
由三角形的外角性质得,∠BEF=∠BAC+∠AGE,
∵∠DFE=2∠BAC,
∴∠BAC=∠AGE,
∴AE=GE,
∵AE=CF,GE=GF,
∴CF=GF,
在Rt△BCF和Rt△BGF中,
,
∴Rt△BCF≌Rt△BGF(HL),
∴BG=BC=2
cm,
∵AG=CG,∠ABC=90°,
∴AC=2BG=2×2
=4
cm,
在Rt△ABC中,AB=
=
=6cm,
所以△ABC的面积=
AB•BC=
×6×2
=6
cm2.
故答案为:6
.
∴∠GAE=∠GCF,
在△AEG和△CFG中,
|
∴△AEG≌△CFG(AAS),
∴AG=CG,GE=GF,
∵BE=BF,
∴BG⊥EF(等腰三角形三线合一),

∵AB∥CD,
∴∠DFE=∠BEF,
由三角形的外角性质得,∠BEF=∠BAC+∠AGE,
∵∠DFE=2∠BAC,
∴∠BAC=∠AGE,
∴AE=GE,
∵AE=CF,GE=GF,
∴CF=GF,
在Rt△BCF和Rt△BGF中,
|
∴Rt△BCF≌Rt△BGF(HL),
∴BG=BC=2
| 3 |
∵AG=CG,∠ABC=90°,
∴AC=2BG=2×2
| 3 |
| 3 |
在Rt△ABC中,AB=
| AC2-BC2 |
(4
|
所以△ABC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
故答案为:6
| 3 |
点评:本题考查了矩形的性质,主要利用了全等三角形的判定与性质,等腰三角形的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,勾股定理,三角形的面积,熟记各性质并最后求出AB的长是解题的关键.

练习册系列答案
相关题目

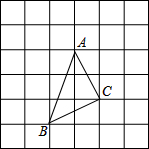 如图,在6×6的方格纸中有一个格点三角形ABC(三角形的顶点都在小正方形的顶点上),每个小正方形的边长都为1.
如图,在6×6的方格纸中有一个格点三角形ABC(三角形的顶点都在小正方形的顶点上),每个小正方形的边长都为1. 如图,在平面直角坐标系xOy中,若菱形ABCD的顶点A,B的坐标分别为(-3,0),(2,0),点D在y轴上,则点C的坐标是
如图,在平面直角坐标系xOy中,若菱形ABCD的顶点A,B的坐标分别为(-3,0),(2,0),点D在y轴上,则点C的坐标是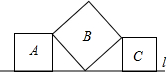 如图,直线l上有三个正方形A,B,C,且正方形A和C的一边在直线l上,正方形B的一个顶点在直线l上,有两个顶点分别与A和C的一个顶点重合,若A和C的面积分别为7和15,则B的面积为
如图,直线l上有三个正方形A,B,C,且正方形A和C的一边在直线l上,正方形B的一个顶点在直线l上,有两个顶点分别与A和C的一个顶点重合,若A和C的面积分别为7和15,则B的面积为