题目内容
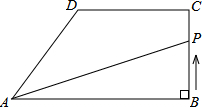 如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=8cm.BC=4cm,CD=5cm.动点P从点B开始沿折线BC-CD-DA以1cm/s的速度运动到点A.设点P运动的时间为t(s),△PAB面积为S(cm2).
如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=8cm.BC=4cm,CD=5cm.动点P从点B开始沿折线BC-CD-DA以1cm/s的速度运动到点A.设点P运动的时间为t(s),△PAB面积为S(cm2).(1)当t=2时,求S的值;
(2)当点P在边DA上运动时,求S关于t的函数表达式;
(3)当S=12时,求t的值.
考点:直角梯形,动点问题的函数图象
专题:几何综合题,动点型
分析:(1)当t=2时,可求出P运动的路程即BP的长,再根据三角形的面积公式计算即可;
(2)当点P在DA上运动时,过D作DH⊥AB,P′M⊥AB,求出P′M的值即为△PAB中AB边上的高,再利用三角形的面积公式计算即可;
(3)当S=12时,则P在BC或AD上运动,利用(1)和(2)中的面积和高的关系求出此时的t即可,
(2)当点P在DA上运动时,过D作DH⊥AB,P′M⊥AB,求出P′M的值即为△PAB中AB边上的高,再利用三角形的面积公式计算即可;
(3)当S=12时,则P在BC或AD上运动,利用(1)和(2)中的面积和高的关系求出此时的t即可,
解答:解:(1)∵动点P以1cm/s的速度运动,
∴当t=2时,BP=2cm,
∴S的值=
AB•BP=
×8×2=8cm2;
(2)过D作DH⊥AB,过P′作P′M⊥AB,
∴P′M∥DH,
∴△AP′M∽△ADH,
∴
=
,
∵AB=8cm,CD=5cm,
∴AH=AB-DC=3cm,
∵BC=4cm,
∴AD=
=5cm,
又∵A′P=14-t,
∴
=
,
∴P′M=
,
∴S=
AB•P′M=
,
即S关于t的函数表达式S=
;
(3)由题意可知当P在CD上运动时,S=
AB×BC=
×8×4=16cm2,
所以当S=12时,P在BC或AD上,
当P在BC上时,12=
×8•t,解得:t=3;
当P在AD上时,12=
,解得:t=
.
∴当S=12时,t的值为3或
.
∴当t=2时,BP=2cm,
∴S的值=
| 1 |
| 2 |
| 1 |
| 2 |
(2)过D作DH⊥AB,过P′作P′M⊥AB,
∴P′M∥DH,
∴△AP′M∽△ADH,
∴
| AP′ |
| AD |
| P′M |
| DH |

∵AB=8cm,CD=5cm,
∴AH=AB-DC=3cm,
∵BC=4cm,
∴AD=
| 32+42 |
又∵A′P=14-t,
∴
| 14-t |
| 5 |
| P′M |
| 4 |
∴P′M=
| 4(14-t) |
| 5 |
∴S=
| 1 |
| 2 |
| 16(14-t) |
| 5 |
即S关于t的函数表达式S=
| 16(14-t) |
| 5 |
(3)由题意可知当P在CD上运动时,S=
| 1 |
| 2 |
| 1 |
| 2 |
所以当S=12时,P在BC或AD上,
当P在BC上时,12=
| 1 |
| 2 |
当P在AD上时,12=
| 16(14-t) |
| 5 |
| 41 |
| 4 |
∴当S=12时,t的值为3或
| 41 |
| 4 |
点评:本题考查了直角梯形的性质、相似三角形的判定和性质以及勾股定理的运用和三角形面积公式的运用,题目的综合性较强,难度中等,对于动点问题特别要注意的是分类讨论数学思想的运用.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
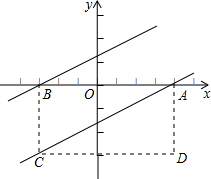 在平面直角坐标系中,矩形ABCD的边AB在x轴上,点A、B的横坐标分别为a+2与2a-5,且关于y轴对称,BC的长为3,且点C在第三象限.
在平面直角坐标系中,矩形ABCD的边AB在x轴上,点A、B的横坐标分别为a+2与2a-5,且关于y轴对称,BC的长为3,且点C在第三象限. 如图,在△ABC中,AB=AC,AB的垂直平分线交BC于D,交AB于G,AC的垂直平分线交BC于E,交AC于F,且BD=DE.
如图,在△ABC中,AB=AC,AB的垂直平分线交BC于D,交AB于G,AC的垂直平分线交BC于E,交AC于F,且BD=DE.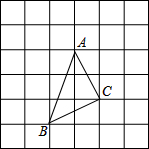 如图,在6×6的方格纸中有一个格点三角形ABC(三角形的顶点都在小正方形的顶点上),每个小正方形的边长都为1.
如图,在6×6的方格纸中有一个格点三角形ABC(三角形的顶点都在小正方形的顶点上),每个小正方形的边长都为1. 如表,给出A、B两种上网宽带的收费方式:
如表,给出A、B两种上网宽带的收费方式: 如图,在平面直角坐标系xOy中,若菱形ABCD的顶点A,B的坐标分别为(-3,0),(2,0),点D在y轴上,则点C的坐标是
如图,在平面直角坐标系xOy中,若菱形ABCD的顶点A,B的坐标分别为(-3,0),(2,0),点D在y轴上,则点C的坐标是