题目内容
12．将4x2+1再加上一项，使它成为（a+b）2的形式（这里a、b指代的是整式或分式），则可以添加的项是4x，-4x，$4{x}^{4}，\frac{1}{16{x}^{2}}$．分析 分①4x2是平方项，②4x2是乘积二倍项，③1是乘积二倍项，然后根据完全平方公式的结构解答．
解答 解：①4x2是平方项时，4x2±4x+1=（2x±1）2，
可加上的单项式可以是4x或-4x，
②当4x2是乘积二倍项时，4x4+4x2+1=（2x2+1）2，
可加上的单项式可以是4x4，
③1是乘积二倍项时，$\frac{1}{16{x}^{2}}+1+4{x}^{2}=（\frac{1}{4x}+2x）^{2}$，
可加上的单项式可以是$\frac{1}{16{x}^{2}}$，
故答案为：4x，-4x，$4{x}^{4}，\frac{1}{16{x}^{2}}$．
点评 本题主要考查了完全平方式，注意分4x2，是平方项与乘积二倍项以及1是乘积二倍项三种情况讨论求解，熟记完全平方公式对解题非常重要．
练习册系列答案
相关题目
20．
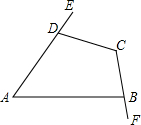如图，下列说法错误的是（ ）
如图，下列说法错误的是（ ）| A． | ∠A与∠EDC是同位角 | B． | ∠A与∠ABF是内错角 | ||
| C． | ∠A与∠ADC是同旁内角 | D． | ∠A与∠C是同旁内角 |
7．下列分式运算或化简错误的是（ ）
| A． | $\frac{1-3x}{-x-2}$=$\frac{3x-1}{x+2}$ | B． | $\frac{-2{x}^{3}y}{4{x}^{2}{y}^{2}}$=-$\frac{x}{2y}$ | ||
| C． | （x2-xy）÷$\frac{x-y}{x}$=（x-y）2 | D． | $\frac{4}{x-2}$+$\frac{x+2}{2-x}$=-1 |
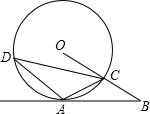已知，如图，A是⊙O上一点，半径OC的延长线与过点A的直线交于B点，OC=BC，AC=$\frac{1}{2}$OB．