题目内容
5．
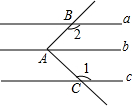如图，直线a∥b∥c，直角∠BAC的顶点A在直线b上，两边分别于直线a、c相交于点B、C，则∠1+∠2的度数是（ ）| A． | 180° | B． | 210° | C． | 270° | D． | 360° |
分析 如图，由平行线的性质可求得∠2+∠3=∠1+∠4=180°，结合条件可求得∠1+∠2．
解答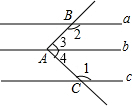 
解：如图，
∵a∥b，
∴∠2+∠3=180°，则∠3=180°-∠2，
∵b∥c，
∴∠1+∠4=180°，则∠4=180°-∠1，
∵∠BAC=90°，
∴∠3+∠4=90°，
∴180°-∠2+180°-∠1=90°，
∴∠1+∠2=270°，
故选C．
点评 本题主要考查平行线的性质，掌握平行线的判定和性质是解题的关键，即①两直线平行?同位角相等，②两直线平行?内错角相等，③两直线平行?同旁内角互补，④a∥b，b∥c⇒a∥c．
练习册系列答案
阅读快车系列答案
相关题目
如图，若AE是△ABC边上的高，∠EAC的角平分线AD交BC于D，∠ACB=40°，求∠ADE．
16．若二次根式$\sqrt{x-2}$有意义，则x的取值范围是（ ）
| A． | x＜2 | B． | x≠2 | C． | x≤2 | D． | x≥2 |
13．
如图，AD，AE分别是△ABC的角平分线和中线，CG⊥AD于F，交AB于G，若AB=8，AC=6，则EF的长为（ ）
如图，AD，AE分别是△ABC的角平分线和中线，CG⊥AD于F，交AB于G，若AB=8，AC=6，则EF的长为（ ）| A． | 2 | B． | $\frac{3}{2}$ | C． | 1 | D． | $\frac{1}{2}$ |
20．
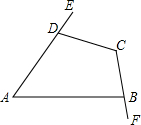如图，下列说法错误的是（ ）
如图，下列说法错误的是（ ）| A． | ∠A与∠EDC是同位角 | B． | ∠A与∠ABF是内错角 | ||
| C． | ∠A与∠ADC是同旁内角 | D． | ∠A与∠C是同旁内角 |
