题目内容

19．若二次函数y=x2+mx的对称轴是x=3，则关于x的方程x2+mx=7的解为（　　）
A．x1=0，x2=6B．x1=1，x2=7C．x1=1，x2=-7D．x1=-1，x2=7

分析 先根据二次函数y=x2+mx的对称轴是x=3求出m的值，再把m的值代入方程x2+mx=7，求出x的值即可．

解答 解：∵二次函数y=x2+mx的对称轴是x=3，
∴-$\frac{m}{2}$=3，解得m=-6，
∴关于x的方程x2+mx=7可化为x2-6x-7=0，即（x+1）（x-7）=0，解得x1=-1，x2=7．
故选D．

点评 本题考查的是二次函数的性质，熟知二次函数的对称轴方程是解答此题的关键．

练习册系列答案
相关题目
9．如图1，在△ABC中，AB=AC，射线BP从BA所在位置开始绕点B顺时针旋转，旋转角为α（0°＜α＜180°）
（1）当∠BAC=60°时，将BP旋转到图2位置，点D在射线BP上．若∠CDP=120°，则∠ACD=∠ABD（填“＞”、“=”、“＜”），线段BD、CD与AD之间的数量关系是BD=CD+AD；
（2）当∠BAC=120°时，将BP旋转到图3位置，点D在射线BP上，若∠CDP=60°，求证：BD-CD=$\sqrt{3}$AD；
（3）将图3中的BP继续旋转，当30°＜α＜180°时，点D是直线BP上一点（点P不在线段BD上），若∠CDP=120°，请直接写出线段BD、CD与AD之间的数量关系（不必证明）
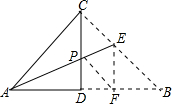10．如图，将一个等腰Rt△ABC对折，使∠A与∠B重合，展开后得折痕CD，再将∠A折叠，使C落在AB上的点F处，展开后，折痕AE交CD于点P，连接PF、EF，下列结论：①tan∠CAE=$\sqrt{2}$-1；②图中共有4对全等三角形；③若将△PEF沿PF翻折，则点E一定落在AB上；④PC=EC；⑤S四边形DFEP=S△APF．正确的个数是（　　）
A．1个B．2个C．3个D．4个
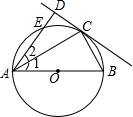7．如图，AB为⊙O的直径，点E在⊙O上，C为$\widehat{BE}$的中点，过点C作直线CD⊥AE于D，连接AC、BC．
（1）试判断直线CD与⊙O的位置关系，并说明理由；
（2）若AD=2，AC=$\sqrt{6}$，求AB的长．
14．若代数式x+2的值为1，则x等于（　　）
A．1B．-1C．3D．-3
4．请从以下两个小题中任选一个作答，若多选，则按第一题计分．
A．一个多边形的一个外角为45°，则这个正多边形的边数是8．
B．运用科学计算器计算：3$\sqrt{17}$sin73°52′≈11.9．（结果精确到0.1）
11．如图，在平面直角坐标系中，一次函数y=kx+b（k≠0）的图象与反比例函数y=$\frac{m}{x}$（m≠0）的图象交于A、B两点，与x轴交于C点，点A的坐标为（n，6），点C的坐标为（-2，0），且tan∠ACO=2．
（1）求该反比例函数和一次函数的解析式；
（2）求点B的坐标．
8．已知反比例函数y=$\frac{6}{x}$，当1＜x＜3时，y的最小整数值是（　　）
A．3B．4C．5D．6
9．分解因式：3x2-x=x（3x-1）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网