题目内容
2. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )| A. | a>0 | B. | c<0 | ||
| C. | 3是方程ax2+bx+c=0的一个根 | D. | 当x<1时,y随x的增大而减小 |
分析 根据二次函数的图象性质可以做出判断.
解答 解:(A)图象开口向下,所以a<0,
故(A)错误;
(B)图象与y轴交点在y轴的正半轴,所以C>0,
故(B)错误;
(C)因为对称轴为x=1,所以(-1,0)与(3,0)关于x=1对称,
故x=3是ax2+bx+c=0的一个根;
故(C)正确;
(D)由图象可知:当x<1时,y随x的增大而增大;
故(D)错误.
故选(C)
点评 本题综合考查二次函数图象的性质,根据图象可得出a、c与0的大小关系,以及图象的变化趋势.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
13. 如图,将矩形ABCD沿EF折叠,使点B,D重合,已知AB=3,AD=4,则
如图,将矩形ABCD沿EF折叠,使点B,D重合,已知AB=3,AD=4,则
①DE=DF;②DF=EF;③△DCF≌△DGE;④EF=$\frac{15}{4}$.
上面结论正确的有( )
 如图,将矩形ABCD沿EF折叠,使点B,D重合,已知AB=3,AD=4,则
如图,将矩形ABCD沿EF折叠,使点B,D重合,已知AB=3,AD=4,则①DE=DF;②DF=EF;③△DCF≌△DGE;④EF=$\frac{15}{4}$.
上面结论正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.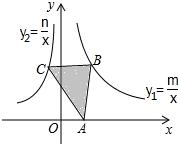 如图,已知△ABC,点A在x轴上,点B在双曲线y1=$\frac{m}{x}$(m>0,x>0)上.点C在双曲线y2=$\frac{n}{x}$(n<0,x<0)上.关于△ABC的面积.下列说法中正确的是( )
如图,已知△ABC,点A在x轴上,点B在双曲线y1=$\frac{m}{x}$(m>0,x>0)上.点C在双曲线y2=$\frac{n}{x}$(n<0,x<0)上.关于△ABC的面积.下列说法中正确的是( )
 如图,已知△ABC,点A在x轴上,点B在双曲线y1=$\frac{m}{x}$(m>0,x>0)上.点C在双曲线y2=$\frac{n}{x}$(n<0,x<0)上.关于△ABC的面积.下列说法中正确的是( )
如图,已知△ABC,点A在x轴上,点B在双曲线y1=$\frac{m}{x}$(m>0,x>0)上.点C在双曲线y2=$\frac{n}{x}$(n<0,x<0)上.关于△ABC的面积.下列说法中正确的是( )| A. | 当点A保持不动,点C,B随意移动时,△ABC的面积不变 | |
| B. | 当点A移动,BC保持不动时,△ABC的面积不变 | |
| C. | 不管点A,B,C怎么移动,△ABC的面积始终不变 | |
| D. | 不管点A,B,C怎么移动,只要BC与x轴平行,△ABC的面积就不变 |
14.若代数式x+2的值为1,则x等于( )
| A. | 1 | B. | -1 | C. | 3 | D. | -3 |
12.化简$\frac{{a}^{2}}{a-1}$-(a+1)的结果是( )
| A. | $\frac{1}{a-1}$ | B. | -$\frac{1}{a-1}$ | C. | $\frac{2a-1}{a-1}$ | D. | -$\frac{2a-1}{a-1}$ |
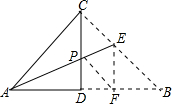 如图,将一个等腰Rt△ABC对折,使∠A与∠B重合,展开后得折痕CD,再将∠A折叠,使C落在AB上的点F处,展开后,折痕AE交CD于点P,连接PF、EF,下列结论:①tan∠CAE=$\sqrt{2}$-1;②图中共有4对全等三角形;③若将△PEF沿PF翻折,则点E一定落在AB上;④PC=EC;⑤S四边形DFEP=S△APF.正确的个数是( )
如图,将一个等腰Rt△ABC对折,使∠A与∠B重合,展开后得折痕CD,再将∠A折叠,使C落在AB上的点F处,展开后,折痕AE交CD于点P,连接PF、EF,下列结论:①tan∠CAE=$\sqrt{2}$-1;②图中共有4对全等三角形;③若将△PEF沿PF翻折,则点E一定落在AB上;④PC=EC;⑤S四边形DFEP=S△APF.正确的个数是( )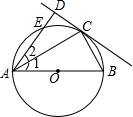 如图,AB为⊙O的直径,点E在⊙O上,C为$\widehat{BE}$的中点,过点C作直线CD⊥AE于D,连接AC、BC.
如图,AB为⊙O的直径,点E在⊙O上,C为$\widehat{BE}$的中点,过点C作直线CD⊥AE于D,连接AC、BC. 如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(-2,0),且tan∠ACO=2.
如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(-2,0),且tan∠ACO=2.