题目内容
4. 在平面直角坐标系xOy中,对称轴为直线x=1的抛物线y=-x2+bx+c与x轴交于点A和点B,与y轴交于点C,且点B的坐标为(-1,0).
在平面直角坐标系xOy中,对称轴为直线x=1的抛物线y=-x2+bx+c与x轴交于点A和点B,与y轴交于点C,且点B的坐标为(-1,0).(1)求抛物线的解析式;
(2)点D的坐标为(0,1),点P是抛物线上的动点,若△PCD是以CD为底的等腰三角形,求点P的坐标.
分析 (1)求出A、B坐标,利用待定点C的坐标为(0,3),点D(1,0),
(2)由点C的坐标为(0,3),点D(1,0),可知满足条件的点P的纵坐标为2,解方程-x2+2x+3=2即可得到点P的横坐标,由此即可解决问题.
解答 解:(1)由题意可求点A的坐标为(3,0).
将点A(3,0)和点B(-1,0)代入y=-x2+bx+c,
得 $\left\{\begin{array}{l}0=-9+3b+c\\ 0=-1-b+c.\end{array}\right.$
解得 $\left\{\begin{array}{l}b=2\\ c=3.\end{array}\right.$
∴抛物线的解析式y=-x2+2x+3.
(2)如图,
∵点C的坐标为(0,3),点D(1,0),
∴满足条件的点P的纵坐标为2.
∴-x2+2x+3=2.
解得 ${x_1}=1+\sqrt{2},{x_2}=1-\sqrt{2}$.
∴点P的坐标为$(1+\sqrt{2},2)$或$(1-\sqrt{2},2)$.
点评 本题考查抛物线与x轴的交点、待定系数法求二次函数的解析式、等腰三角形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
7.某蔬菜经营户从蔬菜批发市场批发蔬菜进行零价,其中西红柿与西兰花的批发价格与零售价格如表.
(1)第一天该经营户批发西红柿和西兰花两种蔬菜共300kg,用去了1520元.这两种蔬菜当天全部售完后,一共能赚多少钱?(请列方程组求解)
(2)第二天该经营户用1520元仍然批发西红柿和西兰花,要想当天全部售完后所赚钱数不少于1050元,则该经营户最多能批发多少千克的西红柿?
| 蔬菜品种 | 西红柿 | 西兰花 |
| 批发价(元/kg) | 3.6 | 8 |
| 零售价(元/kg) | 5.4 | 14 |
(2)第二天该经营户用1520元仍然批发西红柿和西兰花,要想当天全部售完后所赚钱数不少于1050元,则该经营户最多能批发多少千克的西红柿?
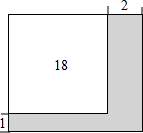 公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图),原空地一边减少了1m,另一边减少了2m,剩余空地的面积为18m2,求原正方形空地的边长.设原正方形的空地的边长xm,则可列方程(x-1)(x-2)=18.
公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图),原空地一边减少了1m,另一边减少了2m,剩余空地的面积为18m2,求原正方形空地的边长.设原正方形的空地的边长xm,则可列方程(x-1)(x-2)=18.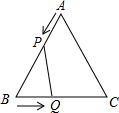 如图所示,已知△ABC是边长为6cm等边三角形,动点P、Q同时从A、B出发,分别在AB、BC方向匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点停止运动,设运动的时间为t (s),解答下列问题:
如图所示,已知△ABC是边长为6cm等边三角形,动点P、Q同时从A、B出发,分别在AB、BC方向匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点停止运动,设运动的时间为t (s),解答下列问题: