题目内容
15．已知3x-4y=0（x，y均不可为0），则$\frac{x}{x+y}$等于$\frac{4}{7}$．分析 根据比例的性质变形，设x=4k，y=3k，代入求出即可．
解答 解：∵3x-4y=0（x，y均不可为0），
∴$\frac{x}{y}$=$\frac{4}{3}$，
设x=4k，y=3k，
∴$\frac{x}{x+y}$=$\frac{4k}{3k+4k}$=$\frac{4}{7}$，
故答案为：$\frac{4}{7}$．
点评 本题考查了比例的性质，能灵活运用比例的性质进行计算是解此题的关键．
练习册系列答案
相关题目
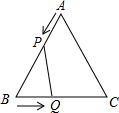如图所示，已知△ABC是边长为6cm等边三角形，动点P、Q同时从A、B出发，分别在AB、BC方向匀速运动，其中点P运动的速度是1cm/s，点Q运动的速度是2cm/s，当点Q到达点C时，P、Q两点停止运动，设运动的时间为t （s），解答下列问题：
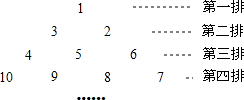将正整数按如图所示的规律排列下去，若有序实数对（n，m）表示第n排，从左到右第m个数，如（4，2）表示正整数9，则（5，2）表示的正整数是12，表示正整数17的有序实数对是（6，5）．
4．若x、y互为倒数，则下列等式正确的是（ ）
| A． | x=-y | B． | xy=-1 | C． | x=$\frac{1}{y}$ | D． | y=±$\frac{1}{x}$ |