题目内容
13.解方程:(1)x2-4x-7=0;
(2)x2-4x-12=0.
分析 (1)首先把常数项移到等号右边,然后利用配方法把方程的左边化为平方的形式,再利用直接开平方法解即可.
(2)首先把方程的左边通过因式分解化为两个一次因式的积的形式,可得(x-6)(x+2)=0,进而可得x-6=0,x+2=0,再解即可.
解答 解:(1)x2-4x=7,
x2-4x+4=7+4,
(x-2)2=11,
x-2=$±\sqrt{11}$,
则x1=2$+\sqrt{11}$,x2=2-$\sqrt{11}$;
(2)x2-4x-12=0
(x-6)(x+2)=0,
则x-6=0,x+2=0,
解得:x1=6,x2=-2.
点评 此题主要考查了一元一次方程的解法--因式分解法,以及开平方法,关键是掌握因式分解法解一元二次方程的一般步骤:①移项,使方程的右边化为零;②将方程的左边分解为两个一次因式的乘积;③令每个因式分别为零,得到两个一元一次方程;④解这两个一元一次方程,它们的解就都是原方程的解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.如图所示,在第一个正方形上加放一根小棒,在此基础上依次加搭正方形,连同第一个在内,共搭了101个正方形,则需要的小棒根数是( )


| A. | 4+101×3 | B. | 4+100×3 | C. | 5+101×3 | D. | 5+100×3 |
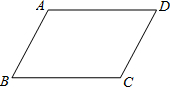 已知:如图,
已知:如图,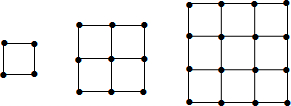
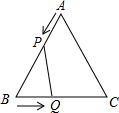 如图所示,已知△ABC是边长为6cm等边三角形,动点P、Q同时从A、B出发,分别在AB、BC方向匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点停止运动,设运动的时间为t (s),解答下列问题:
如图所示,已知△ABC是边长为6cm等边三角形,动点P、Q同时从A、B出发,分别在AB、BC方向匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点停止运动,设运动的时间为t (s),解答下列问题: