题目内容
12.若$\sqrt{{a}^{2}-2a+1}$+b2+2b+1=0,则a2+$\frac{1}{{a}^{2}}$-|b|=1.分析 首先利用完全平方公式变形得出$\sqrt{(a-1)^{2}}$+(b+1)2=0,利用非负数的性质得出a=1,b=-1,进一步代入求得答案即可.
解答 解:∵$\sqrt{{a}^{2}-2a+1}$+b2+2b+1=0,
∴$\sqrt{(a-1)^{2}}$+(b+1)2=0,
∴a-1=0,b+1=0,
∴a=1,b=-1,
∴a2+$\frac{1}{{a}^{2}}$-|b|=1.
故答案为:1.
点评 此题考查了配方法的应用,以及非负数的性质,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
20.关于x的方程x2+(2a2+a-$\sqrt{2{a}^{2}+a+6}$)x+a=0的两实数根互为相反数,则a=( )
| A. | -$\frac{3}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{1}{2}$ |
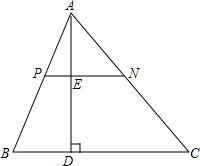 已知:如图所示,PN∥BC,AD⊥BC交PN于点E,交BC于点D.
已知:如图所示,PN∥BC,AD⊥BC交PN于点E,交BC于点D.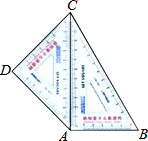 如图,学生用三角板中,等腰直角三角形三角板的斜边靠在另一个含60°角的三角形板的对边上恰好完全重合,拼成一个四边形ABCD.若60°所对的直角边长为12cm,求拼成四边形ABCD的面积.
如图,学生用三角板中,等腰直角三角形三角板的斜边靠在另一个含60°角的三角形板的对边上恰好完全重合,拼成一个四边形ABCD.若60°所对的直角边长为12cm,求拼成四边形ABCD的面积.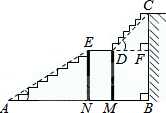 某宾馆大厅到二楼的楼梯设计图如下,已知BC=6米,AB=9米,中间平台宽度DE为2米.DM、DN为平台的两根支柱,DM、EN垂直于AB,垂足分别为M、N,∠EAB=30°,∠CDF=45°.求DM和BC的水平距离BM.
某宾馆大厅到二楼的楼梯设计图如下,已知BC=6米,AB=9米,中间平台宽度DE为2米.DM、DN为平台的两根支柱,DM、EN垂直于AB,垂足分别为M、N,∠EAB=30°,∠CDF=45°.求DM和BC的水平距离BM.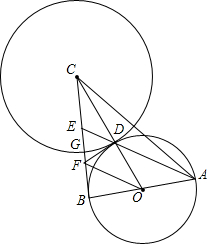 如图:Rt△ABC中,∠ABC=90°,AB=BC,以AB为直径的⊙O交OC于D,AD的延长线交BC于E,过点D作⊙O的切线DF交BC于F,连接OF.⊙C切⊙O于点D,交BC于G
如图:Rt△ABC中,∠ABC=90°,AB=BC,以AB为直径的⊙O交OC于D,AD的延长线交BC于E,过点D作⊙O的切线DF交BC于F,连接OF.⊙C切⊙O于点D,交BC于G 如图,BD为⊙O的直径,AB=AC,AD交BC于点E,延长DB交⊙O的切线AF于点F,AE=2,ED=4.
如图,BD为⊙O的直径,AB=AC,AD交BC于点E,延长DB交⊙O的切线AF于点F,AE=2,ED=4.