题目内容
20.关于x的方程x2+(2a2+a-$\sqrt{2{a}^{2}+a+6}$)x+a=0的两实数根互为相反数,则a=( )| A. | -$\frac{3}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{1}{2}$ |
分析 利用根与系数的关系得出x1+x2=-(2a2+a-$\sqrt{2{a}^{2}+a+6}$)=0,进而求出即可,注意一元二次方程根的情况确定方法.
解答 解:∵关于x的方程x2+(2a2+a-$\sqrt{2{a}^{2}+a+6}$)x+a=0的两个根互为相反数,
∴x1+x2=0,即:x1+x2=-(2a2+a-$\sqrt{2{a}^{2}+a+6}$)=0,
解得:a=1或-$\frac{3}{2}$,
当a=1时,
4x2+1=0,
4x2=-1,
故a=5不合题意舍去,
故a=-$\frac{3}{2}$,
故选:A.
点评 此题主要考查了根与系数的关系以及一元二次方程根的求法等知识,此题容易忽略a=1时方程无解.

练习册系列答案
相关题目
5.在一次质检抽测中,随机抽取某摊位10袋食盐,测得各袋的质量分别为(单位:g)
501,502,504,496,497,503,496,500,501,499
根据以上抽测结果,任买一袋该摊位的食盐,质量在497.5g~501.5g之间的概率为( )
501,502,504,496,497,503,496,500,501,499
根据以上抽测结果,任买一袋该摊位的食盐,质量在497.5g~501.5g之间的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{10}$ | D. | $\frac{2}{5}$ |
10. 如图,点S是⊙O的直径AB延长线上的一点,SC与⊙O相切于点C.若∠S=30°,则∠A等于( )
如图,点S是⊙O的直径AB延长线上的一点,SC与⊙O相切于点C.若∠S=30°,则∠A等于( )
 如图,点S是⊙O的直径AB延长线上的一点,SC与⊙O相切于点C.若∠S=30°,则∠A等于( )
如图,点S是⊙O的直径AB延长线上的一点,SC与⊙O相切于点C.若∠S=30°,则∠A等于( )| A. | 20° | B. | 30° | C. | 35° | D. | 40° |
 在△ABC中,∠ADC=∠ACB,AD=9,DB=3,求AC的长.
在△ABC中,∠ADC=∠ACB,AD=9,DB=3,求AC的长.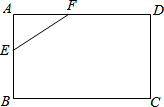 如图所示,将长方形ABCD切去一角后得到的五边形BCDEF的五条边长是17、19、23、27和38(顺序不一定按此排列),则五边形的面积是966.
如图所示,将长方形ABCD切去一角后得到的五边形BCDEF的五条边长是17、19、23、27和38(顺序不一定按此排列),则五边形的面积是966.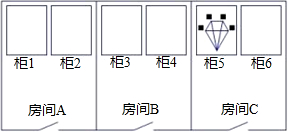 如图,有三间房,每间房内放有两个柜子,仅有一件宝物藏在某个柜子中,寻宝游戏规则如下:只允许进入三个房间中的一个房间并打开其中一个柜子即为一次游戏结束.找到宝物为游戏胜出,否则为游戏失败.
如图,有三间房,每间房内放有两个柜子,仅有一件宝物藏在某个柜子中,寻宝游戏规则如下:只允许进入三个房间中的一个房间并打开其中一个柜子即为一次游戏结束.找到宝物为游戏胜出,否则为游戏失败. 如图,正方体的棱长和圆柱直径均为1,且圆柱的高为2,则这个组合体右视图的面积是2.
如图,正方体的棱长和圆柱直径均为1,且圆柱的高为2,则这个组合体右视图的面积是2.