题目内容
7.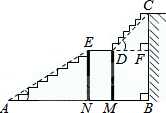 某宾馆大厅到二楼的楼梯设计图如下,已知BC=6米,AB=9米,中间平台宽度DE为2米.DM、DN为平台的两根支柱,DM、EN垂直于AB,垂足分别为M、N,∠EAB=30°,∠CDF=45°.求DM和BC的水平距离BM.
某宾馆大厅到二楼的楼梯设计图如下,已知BC=6米,AB=9米,中间平台宽度DE为2米.DM、DN为平台的两根支柱,DM、EN垂直于AB,垂足分别为M、N,∠EAB=30°,∠CDF=45°.求DM和BC的水平距离BM.(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)(sin30°=$\frac{1}{2}$,cos30°=$\frac{\sqrt{3}}{2}$,tan30°=$\frac{\sqrt{3}}{3}$,sin45°=$\frac{\sqrt{2}}{2}$,cos45°=$\frac{\sqrt{2}}{2}$)
分析 设BM=x米.由等腰直角三角形的性质知,CF=DF=x,得EN=FB=BC-CF=6-x,AN=AB-DF-ED=7-x,则在直角三角形ANE中,有EN=AN•tan30°,建立方程求得x的值.
解答 解:设BM=x米.
∵∠CDF=45°,∠CFD=90°,
∴CF=DF=x米,
∴BF=BC-CF=(6-x)米.
∴EN=DM=BF=(6-x)米.
∵AB=9米,DE=2米,BM=DF=x米,
∴AN=AB-MN-BM=(7-x)米.
在△AEN中,∠ANE=90°,∠EAN=30°,
∴EN=AN•tan30°.
即6-x=$\frac{\sqrt{3}}{3}$(7-x).
解这个方程得:x=$\frac{18-7\sqrt{3}}{3-\sqrt{3}}$≈4.6.
答:DM和BC的水平距离BM的长度约为4.6米.
点评 此题主要考查了解直角三角形的应用,本题通过设适当的参数,利用直角三角形的边角关系建立方程而求解是解题关键.

练习册系列答案
相关题目
18.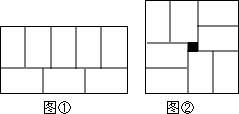 用8块相同的长方形地砖拼矩形,小明拼成了图①,小红拼成了图②,小红所拼图形中间刚好多出一个边长为1的小正方形,则每个小长方形的长宽分别为( )
用8块相同的长方形地砖拼矩形,小明拼成了图①,小红拼成了图②,小红所拼图形中间刚好多出一个边长为1的小正方形,则每个小长方形的长宽分别为( )
 用8块相同的长方形地砖拼矩形,小明拼成了图①,小红拼成了图②,小红所拼图形中间刚好多出一个边长为1的小正方形,则每个小长方形的长宽分别为( )
用8块相同的长方形地砖拼矩形,小明拼成了图①,小红拼成了图②,小红所拼图形中间刚好多出一个边长为1的小正方形,则每个小长方形的长宽分别为( )| A. | 10,6 | B. | 15,9 | C. | 5,3 | D. | 20,12 |
2.已知实数a、b满足a2=2-2a,b2=2-2b,则$\frac{b}{{a}^{2}}$+$\frac{a}{{b}^{2}}$=( )
| A. | 5 | B. | 1±$\sqrt{3}$ | C. | 5或1-$\sqrt{3}$ | D. | 5或1±$\sqrt{3}$ |
19.人的大脑每天能记录大约8600万条信息,8600万用科学记数法表示为( )
| A. | 0.86×108 | B. | 8.6×103 | C. | 8.6×107 | D. | 86×102 |
16.已知反比例函数y=-$\frac{k}{x}$图象上三个点的坐标分别是A(-2,y1)、B(-1,y2)、C(2,y3),若y1<y2,则( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y1<y2 | D. | y3=y1<y2 |
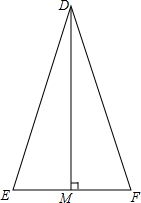 如图所示,在等腰三角形DEF中,腰DE=DF=2$\sqrt{10}$,底边EF=4,DM⊥EF,交EF于点M.
如图所示,在等腰三角形DEF中,腰DE=DF=2$\sqrt{10}$,底边EF=4,DM⊥EF,交EF于点M. 如图,正方体的棱长和圆柱直径均为1,且圆柱的高为2,则这个组合体右视图的面积是2.
如图,正方体的棱长和圆柱直径均为1,且圆柱的高为2,则这个组合体右视图的面积是2.