题目内容
2.已知等式$\frac{\sqrt{(3-x)^{2}}}{3-x}$+$\sqrt{x-3}$=0,则x=4.分析 根据二次根式的性质,可化简方程,根据解无理方程,可得答案.
解答 解:由$\frac{\sqrt{(3-x)^{2}}}{3-x}$+$\sqrt{x-3}$=0,得
$\frac{x-3}{3-x}$+$\sqrt{x-3}$=0,
$\sqrt{x-3}$=1,
解得x=4.
故答案为:4.
点评 本题考查了二次根式的性质与化简,利用二次根式的性质化简方程是解题关键.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
7.把连续奇数列成下表:
(1)表中的m值是19:
(2)第6行、第5列的数字是65;
(3)请用一个长方形方框框住表中的四个数字,交叉相乘,再将乘积相减.看看你能发现什么结论,用文字语言表述你的结论.并用整式运算证明你的结论.
| 第一列 | 第二列 | 第三列 | 第四列 | 第五列 | 第六列 | 第七列 | |
| 第1行 | 1 | 3 | 5 | 7 | 9 | 11 | 13 |
| 第2行 | 15 | 17 | m | 21 | 23 | 25 | 27 |
| 第3行 | 29 | 31 | 33 | 35 | 37 | 39 | 41 |
| 第4行 | 43 | 45 | 47 | 49 | 51 | 53 | 55 |
| … |
(2)第6行、第5列的数字是65;
(3)请用一个长方形方框框住表中的四个数字,交叉相乘,再将乘积相减.看看你能发现什么结论,用文字语言表述你的结论.并用整式运算证明你的结论.
13.下列说法正确的是( )
| A. | 互为相反数的两数均为一正一负 | B. | 1是最小的正整数 | ||
| C. | 有理数包含正有理数与负有理数 | D. | 一个数的绝对值是正数 |
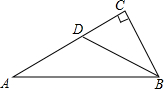 如图所示,在△ABC中,∠C=90°,tanA=$\frac{1}{2}$,D是AC上一点,∠CBD=∠A,sin∠CDB=$\frac{2\sqrt{5}}{5}$.
如图所示,在△ABC中,∠C=90°,tanA=$\frac{1}{2}$,D是AC上一点,∠CBD=∠A,sin∠CDB=$\frac{2\sqrt{5}}{5}$.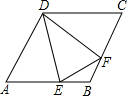 如图,在菱形ABCD中,点E、F分别是AB和BC上的点,且BE=BF,求证:△ADE≌△CDF.
如图,在菱形ABCD中,点E、F分别是AB和BC上的点,且BE=BF,求证:△ADE≌△CDF.