题目内容
17.已知P是直线y=-$\frac{4}{3}$x+4上的一个动点,以P为圆心作圆,若⊙P的半径为$\frac{12}{5}$,且⊙P与坐标轴有个公共点,设点P横坐标为a,则a的取值范围是-$\frac{12}{5}$≤a≤$\frac{24}{5}$.分析 首先求出直线与坐标轴的交点坐标,由勾股定理求出AB,由三角形的面积求出OC,再求出⊙P与y轴和与x轴相切时的a的值,即可得出结果.
解答 解:如图所示:
直线y=-$\frac{4}{3}$x+4,当x=0时,y=4;当y=0时,x=3;
∴A(3,0),B(0,4),
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
作OC⊥AB于C,则OC=$\frac{3×4}{5}$=$\frac{12}{5}$,
∴当P与C重合时,⊙P与坐标轴有交点,
当⊙P与y轴相切时,a=-$\frac{12}{5}$;
当⊙P与x轴相切时,-$\frac{4}{3}$x+4=-$\frac{12}{5}$,
解得:x=$\frac{24}{5}$,即a=$\frac{24}{5}$,
∴⊙P与坐标轴有个公共点,设点P横坐标为a,则a的取值范围是-$\frac{12}{5}$≤a≤$\frac{24}{5}$;
故答案为:-$\frac{12}{5}$≤a≤$\frac{24}{5}$.
点评 本题考查了直线与圆的位置关系、勾股定理、一次函数图象上点的坐标特征;求出⊙P与y轴和与x轴相切时的a的值是解决问题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 已知二次函数的图象经过(0,-3),且顶点坐标为(-1,-4).
已知二次函数的图象经过(0,-3),且顶点坐标为(-1,-4). 矩形ABCD的两条对角线相交于点O,∠AOB=60°,AC=4cm,则AB=2cm,矩形ABCD的面积=4$\sqrt{3}$cm2.
矩形ABCD的两条对角线相交于点O,∠AOB=60°,AC=4cm,则AB=2cm,矩形ABCD的面积=4$\sqrt{3}$cm2.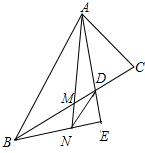 如图,已知△ABC中,M是BC的中点,AD平分∠A,B在AD上的射影为E,EB交AM于N,求证:DN∥AB.
如图,已知△ABC中,M是BC的中点,AD平分∠A,B在AD上的射影为E,EB交AM于N,求证:DN∥AB.