题目内容
16.如图1,△ABC和△CDE均为等腰三角形,AC=BC,CD=CE,AC>CD,∠ACB=∠DCE且点A、D、E在同一直线上,连接BE.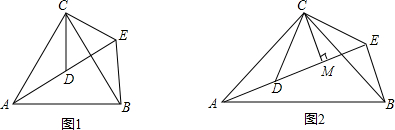
(1)若∠ACB=60°,则∠AEB的度数为60°;线段AD、BE之间的数量关系是相等;
(2)若∠ACB=n°,用n表示∠AEB并说明理由;
(3)如图2,若∠ACB=∠DCE=90°,点M是DE的中点.若CM=7,BE=10,试求AB的长.(请写全必要的证明和计算过程)
分析 (1)易证∠ACD=∠BCE,即可证明△ACD≌△BCE,可得∠CDA=∠CEB,AD=BE,根据∠CDA=180°-∠CDE和∠CED=60°,即可求得∠AEB的值,即可解题;
(2)如图1,根据已知条件∠ACB=∠DCE,求得∠ACD=∠BCE,推出△ACD≌△BCE(SAS),根据全等三角形的性质即可得到结论;
(3)如图2,根据等腰直角三角形的性质得到DE=2CM=14,由于∠ACB=∠DCE=90°,得到∠ACD=∠BCE,证得△ACD≌△BCE,根据全等三角形的性质得到AD=BE=10,∠CAD=∠CBE,根据三角形的内角和得到∠AEB=∠ACH=90°,根据勾股定理即可得到结论;
解答 解:(1)∵∠ACD+∠DCB=60°,∠DCB+∠BCE=60°,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE(SAS),
∴∠CDA=∠CEB,AD=BE,
∵∠CDA=180°-∠CDE=120°,∠CED=60°,
∴∠AEB=120°-60°=60°;
故答案为:60°,相等;
(2)如图1, ∵∠ACB=∠DCE,
∵∠ACB=∠DCE,
∴∠ACD+∠DCB=∠DCB+∠BCE,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE(SAS),
∴∠CAD=∠CBE,
∵∠AHC=∠BHE,
∴∠AEB=∠ACB=n;
(3)如图2,∵点M是DE的中点,
∴CM=DM,
∵△CDE是等腰直角三角形,
∴CM⊥DE,CM=DM=7,
∴DE=2CM=14,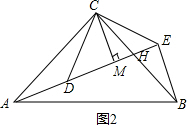
∵∠ACB=∠DCE=90°,
∴∠ACD=∠BCE,
在△ACD与△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE,
∴AD=BE=10,∠CAD=∠CBE,
∵∠AHC=∠BHE,
∴∠AEB=∠ACH=90°,
∵AE=AD+DE=24,
∴AB=$\sqrt{A{E}^{2}+B{E}^{2}}$=$\sqrt{2{4}^{2}+1{0}^{2}}$=26.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质,等腰三角形的性质,勾股定理,三角形的内角和,本题中求证△ACD≌△BCE是解题的关键.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案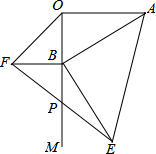 如图,AO⊥OM,OA=8,点B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF、等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,PB的长度是( )
如图,AO⊥OM,OA=8,点B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF、等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,PB的长度是( )| A. | 3.6 | B. | 4 | ||
| C. | 4.8 | D. | PB的长度随B点的运动而变化 |
 如图,将正方形OABC放在平面直角坐标系中,点A的坐标为(1,2),则点B的坐标是(-1,3).
如图,将正方形OABC放在平面直角坐标系中,点A的坐标为(1,2),则点B的坐标是(-1,3). 如图所示,在△ABC中:
如图所示,在△ABC中: 如图,在梯形ABCD中,AD∥BC,S△AOD:S△BOC=1:9.
如图,在梯形ABCD中,AD∥BC,S△AOD:S△BOC=1:9.