Question

2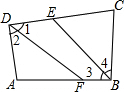．如图，在四边形ABCD中，∠ABC、∠ADC的平分线分别与CD、AB相交于点E、F．
（1）若∠A与∠C互补，∠CDF=36°，求∠ABE=54°．
（2）探索当∠A与∠C满足什么关系时，BE与DF平行，并请说明理由．

Answer 1

分析 （1）根据四边形内角和得到∠ABC+∠ADC=180°，再根据角平分线定义得到∠ABE=$\frac{1}{2}$ABC，∠CDF=$\frac{1}{2}$ADC，而∠CDF=40°，则∠ADC=72°，所以2∠ABE+72°=180°，解得∠ABE=54°；
（2）根据四边形内角和得到∠ABC+∠ADC=180°，再根据角平分线定义得到∠ABE=$\frac{1}{2}$∠ABC，∠ADF=$\frac{1}{2}$∠ADC，则∠ABE+∠ADF=90°，加上∠AFD+∠ADF=90°，利用等角的余角相等得∠AFD=∠ABE，然后根据平行线的判定定理得到DF∥BE．

解答 解：（1）∵∠A与∠C互补，
∴∠ADC+∠CBA=180°，
∵∠ABC、∠ADC的平分线分别与CD、AB相交于点E、F．
∴∠ADC=2∠1=2×36°=72°，∠ABC=2∠3，
∴72°+2∠3=180°，
∴∠3=54°．
故答案为54°；

（2）当∠A=∠C=90°时，DF∥BE，
∵在四边形ABCD中，∠A=∠C=90°，
∴∠ABC+∠ADC=180°，
∵∠ABC、∠ADC的平分线分别与CD、AB相交于点E、F．
∴∠ABE=$\frac{1}{2}$∠ABC，∠ADF=$\frac{1}{2}$∠ADC，
∴∠ABE+∠ADF=90°，
∵∠AFD+∠ADF=90°，
∴∠AFD=∠ABE，
∴DF∥BE．

点评 本题考查了平行线的判定与性质：平行线的判定是由角的数量关系判断两直线的位置关系．平行线的性质是由平行关系来寻找角的数量关系．应用平行线的判定和性质定理时，一定要弄清题设和结论，切莫混淆．