题目内容
15.分别以矩形ABCD的边AD和CD为一边,向矩形外作正三角形ADE和正三角形CDF,连接BE和BF.求证:BE=BF.
分析 首先根据等边三角形的性质求得△FCB≌△BAE,得到BE=BF.
解答  证明:∵四边形ABCD 为矩形,
证明:∵四边形ABCD 为矩形,
∴AB=CD,AD=BC,∠BAD=∠DCB=90°,
∵△ADE和△CDF是等边三角形,
∴∠EAD=∠DCF=60°,DC=FC,AE=AD,
∴∠BAE=∠BCF=150°AB=CF,
∴AE=BC,
在△ABE与△CBF中,
$\left\{\begin{array}{l}{AB=CF}\\{∠BAE=∠BCF}\\{AE=BC}\end{array}\right.$,
∴△ABE≌△CBF,
∴BE=BF.
点评 本题考查了矩形的性质,等边三角形的性质,等腰三角形的性质,解答时求出∠BAE=∠BCF=150°很关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4. 如图,⊙O是△ABC的外接圆,已知∠A=30°,BC=2,则⊙O的半径为( )
如图,⊙O是△ABC的外接圆,已知∠A=30°,BC=2,则⊙O的半径为( )
 如图,⊙O是△ABC的外接圆,已知∠A=30°,BC=2,则⊙O的半径为( )
如图,⊙O是△ABC的外接圆,已知∠A=30°,BC=2,则⊙O的半径为( )| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 4 |
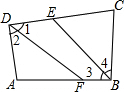 如图,在四边形ABCD中,∠ABC、∠ADC的平分线分别与CD、AB相交于点E、F.
如图,在四边形ABCD中,∠ABC、∠ADC的平分线分别与CD、AB相交于点E、F.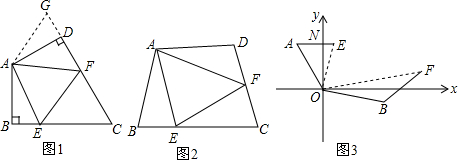
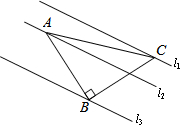 如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为7,l2,l3之间的距离为8,求AC的长.
如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为7,l2,l3之间的距离为8,求AC的长. 已知三角形ABC、点D,过点D作三角形ABC平移后的图形,使D点与A点为对应点.
已知三角形ABC、点D,过点D作三角形ABC平移后的图形,使D点与A点为对应点.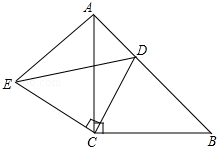 已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为AB边上一点.猜想BD2、AD2、CD2之间的关系,并证明.
已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为AB边上一点.猜想BD2、AD2、CD2之间的关系,并证明.