题目内容
12．若$\frac{a}{b}$=$\frac{c}{d}$=$\frac{5}{7}$（2b-3d≠0），则$\frac{2a-3c}{2b-3d}$=$\frac{5}{7}$．分析 根据比的性质，比的前项后项都乘以或除以同一个不为零的数，比值不变，可得$\frac{2a}{2b}$与$\frac{3c}{3d}$的关系，根据等比性质，可得答案．
解答 解：由比的性质，得$\frac{2a}{2b}$=$\frac{3c}{3d}$=$\frac{5}{7}$，
由等比性质，得$\frac{2a-3c}{2b-3d}$=$\frac{5}{7}$，
故答案为：$\frac{5}{7}$．
点评 本题考查了比例的性质，利用了比的性质，等比性质：$\frac{a}{b}$=$\frac{c}{d}$⇒$\frac{a-c}{b-d}$=$\frac{a}{b}$．
练习册系列答案
相关题目
如图，Rt△ABC中，BD是斜边AC上的高线，E，F分别是AC，AB上的点，若∠1=∠2，则EF∥BD．试说明理由．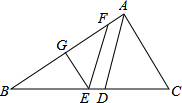
已知△ABC，∠BAC=80°，AD平分∠BAC，E在BC上，过E分别作EF∥AD交AB于F，作EG∥AC交AB于G，则∠GEF=40°．
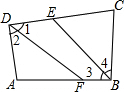如图，在四边形ABCD中，∠ABC、∠ADC的平分线分别与CD、AB相交于点E、F．