题目内容
6.某水果店老板准备去水果批发市场批发甲、乙两种水果,该批发市场时成袋批发,每袋10千克,甲水果批发价6元/千克,最少批发20千克,在此基础上,每多批发10千克,批发价降低0.3元/千克;乙水果批发价4元/千克,最少批发30千克,在此基础上,每多批发10千克,批发价降低0.2元/千克.(例:购买甲水果30千克时,批发价为5.7元/千克),设水果店老板在最少批发的基础上,多批发甲水果x袋,多批发乙水果y袋,根据上述材料,回答以下问题:(1)根据题意,完成下了表格:
| 甲水果 | 乙水果 | |
| 数量(千克) | 20+10x | 30+10y |
| 批发价(元/千克) | 6-0.3x | 4-0.2y |
(3)老板考虑到自己只带了400元,最后决定购买甲、乙两两种水果共90千克(批发甲水果需要超过20千克,乙水果需超过30千克),请你帮助水果店老板设计批发方案.
分析 (1)由批发价格与购买量的关系可用得出表格中的数据;
(2)由甲、乙批发价格相同以及总批发量可用得出关于x、y的二元一次方程组,解方程组即可得出结论;
(3)设甲水果批发a袋,则乙水果批发(9-a)袋,由总价格=单价×数量得出总价w关于a的函数关系式,由a的取值范围可得出购买方案,算出总价后与400进行比较,即可得出结论.
解答 解:(1)根据题意可知:批发甲种水果20+10x千克,乙种水果30+10y千克,甲种水果的批发单价为6-0.3x,乙种水果的批发单价为4-0.2y.
故答案为:30+10y;6-0.3x.
(2)由题意得:$\left\{\begin{array}{l}{20+10x+30+10y=150}\\{6-0.3x=4-0.2y}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=8}\\{y=2}\end{array}\right.$.
20+10×8=100(千克),30+10×2=50(千克).
答:批发甲种水果100千克,乙种水果50千克.
(3)设甲水果批发a袋,则乙水果批发(9-a)袋,
总价w=10a[6-0.3(a-2)]+10(9-a)[4-0.2(9-a-3)]=-5a2+56a+252,
由$\left\{\begin{array}{l}{a>2}\\{9-a>3}\end{array}\right.$,可知2<a<6,
∴a=2,3,4.
方案一:a=3,即批发甲种水果30kg,乙种水果60kg,w=-5×32+56×3+252=375(元);
方案二:a=4,即批发甲种水果40kg,乙种水果50kg,w=-5×42+56×4+252=396(元);
方案三:a=5,即批发甲种水果50kg,乙种水果40kg,w=-5×52+56×5+252=407>400,舍去.
点评 本题考查了一元一次不等式组的应用以及二元一次方程组的应用,解题的关键是:(1)明白各数量之间的关系;(2)列出关于x、y的二元一次方程组;(3)解一元一次不等式组得出a的取值范围.本题属于中档题,难度不大,解决该类型题目时,由各数量关系列出方程(或方程组)是关键.

 ABC考王全优卷系列答案
ABC考王全优卷系列答案| A. | 1:$\sqrt{3}$ | B. | $\sqrt{3}$:1 | C. | 1:$\sqrt{2}$ | D. | $\sqrt{2}$:1 |
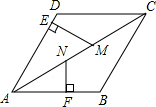 如图,在菱形ABCD中,点M、N在AC上,ME⊥AD,NF⊥AB,若NF=NM=2,ME=3,则AM=6.
如图,在菱形ABCD中,点M、N在AC上,ME⊥AD,NF⊥AB,若NF=NM=2,ME=3,则AM=6.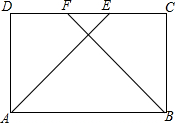 四边形ABCD中,AB∥CD,AB=CD,AE为∠A的平分线,BF为∠B的平分线,E、F在CD上,AE=BF,证明:四边形ABCD是矩形.
四边形ABCD中,AB∥CD,AB=CD,AE为∠A的平分线,BF为∠B的平分线,E、F在CD上,AE=BF,证明:四边形ABCD是矩形.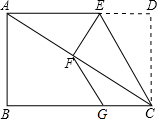 如图,已知点E是矩形一边AD上的一点,沿CE折叠矩形使点D落在对角线AC上的点F处,点G为BC上一点,且CG=DE,连FG.
如图,已知点E是矩形一边AD上的一点,沿CE折叠矩形使点D落在对角线AC上的点F处,点G为BC上一点,且CG=DE,连FG. 如图,在△ABC中,AD为∠BAC的平分线,过D作DE∥AB,交AC于E点,在AB上取BF=AE,求证:FE∥BC.
如图,在△ABC中,AD为∠BAC的平分线,过D作DE∥AB,交AC于E点,在AB上取BF=AE,求证:FE∥BC.