题目内容
1.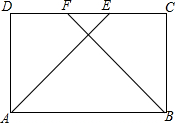 四边形ABCD中,AB∥CD,AB=CD,AE为∠A的平分线,BF为∠B的平分线,E、F在CD上,AE=BF,证明:四边形ABCD是矩形.
四边形ABCD中,AB∥CD,AB=CD,AE为∠A的平分线,BF为∠B的平分线,E、F在CD上,AE=BF,证明:四边形ABCD是矩形.
分析 根据角平分线的性质结合平行线的性质得出AD=DE,CF=CB,进而得出△ADE≌△BCF(SSS),进而得出∠C=∠D=90°,则平行四边形ABCD是矩形.
解答 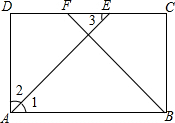 证明:∵AB∥CD,AB=CD,
证明:∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∵AE为∠A的平分线,BF为∠B的平分线,
∴∠1=∠2,∠CBF=∠FBA,
又∵AB∥CD,
∴∠1=∠3,
∴AD=DE,
同理可得:CF=CB,
故AD=DE=BC=FC,
在△ADE和△BCF中,
$\left\{\begin{array}{l}{AD=BC}\\{DE=FC}\\{AE=BF}\end{array}\right.$,
∴△ADE≌△BCF(SSS),
∴∠D=∠C,
又∵AD∥BC,
∴∠C+∠D=180°,
∴∠C=∠D=90°,
∴平行四边形ABCD是矩形.
点评 此题主要考查了矩形的判定以及全等三角形的判定与性质,正确得出△ADE≌△BCF(SSS)是解题关键.

练习册系列答案
相关题目
11.下列各数中不是分数的是( )
| A. | -0.2 | B. | $\frac{3}{2}$ | C. | $\sqrt{2}$ | D. | 25% |
9.下列函数中,当x>0时,y随x增大而增大的是( )
| A. | y=-x | B. | y=$\frac{1}{x}$ | C. | y=3-2x | D. | y=x2 |
16.下列关于多边形的说法不正确的是( )
| A. | 内角和与外角和相等的多边形是四边形 | |
| B. | 十边形的内角和为1440° | |
| C. | 多边形的内角中最多有四个直角 | |
| D. | 十边形共有40条对角线 |
6.某水果店老板准备去水果批发市场批发甲、乙两种水果,该批发市场时成袋批发,每袋10千克,甲水果批发价6元/千克,最少批发20千克,在此基础上,每多批发10千克,批发价降低0.3元/千克;乙水果批发价4元/千克,最少批发30千克,在此基础上,每多批发10千克,批发价降低0.2元/千克.(例:购买甲水果30千克时,批发价为5.7元/千克),设水果店老板在最少批发的基础上,多批发甲水果x袋,多批发乙水果y袋,根据上述材料,回答以下问题:
(1)根据题意,完成下了表格:
(2)当水果店老板批发甲、乙两种水果共150千克时,甲、乙两种水果批发价相同,问此时分别批发甲、乙两种水果多少千克?
(3)老板考虑到自己只带了400元,最后决定购买甲、乙两两种水果共90千克(批发甲水果需要超过20千克,乙水果需超过30千克),请你帮助水果店老板设计批发方案.
(1)根据题意,完成下了表格:
| 甲水果 | 乙水果 | |
| 数量(千克) | 20+10x | 30+10y |
| 批发价(元/千克) | 6-0.3x | 4-0.2y |
(3)老板考虑到自己只带了400元,最后决定购买甲、乙两两种水果共90千克(批发甲水果需要超过20千克,乙水果需超过30千克),请你帮助水果店老板设计批发方案.
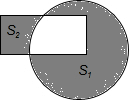 如图,在半径为4的圆中,阴影部分图形的面积为S1;在边长为4,2的矩形中,阴影部分的面积为S2,则S1-S2的值为16π-8.(结果保留π)
如图,在半径为4的圆中,阴影部分图形的面积为S1;在边长为4,2的矩形中,阴影部分的面积为S2,则S1-S2的值为16π-8.(结果保留π)