题目内容
1.如图,△ABC是一块直角三角形余料,∠C=90°,AC=6,BC=8,现在要把它加工成一个正方形零件,试说明下面哪种加工方法利用率高?
分析 方法一:当所截的正方形的边在△ABC的直角边上,如图1,设正方形CDEF边长为x,则CD=DE=x,AD=AC-CD=6-x,先证明△ADE∽△ACB,于是可利用相似比求得x=$\frac{24}{7}$;
方法二:当所截的正方形的边在△ABC的斜边上,如图2,作CM⊥AB于M,交CD于N,先利用勾股定理计算出AB=10,再利用面积法计算出CM=$\frac{24}{5}$,设正方形DEFG边长为x,则DG=MNx,CN=$\frac{24}{5}$-x,接着证明△CDG∽△CAB,则可利用相似比计算出x=$\frac{120}{37}$,然后比较两个正方形的边长的大小来判断利用率高低.
解答 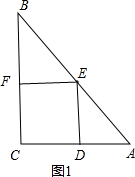 解:方法一:当所截的正方形的边在△ABC的直角边上,如图1,设正方形CDEF边长为x,则CD=DE=x,AD=AC-CD=6-x,
解:方法一:当所截的正方形的边在△ABC的直角边上,如图1,设正方形CDEF边长为x,则CD=DE=x,AD=AC-CD=6-x,
∵DE∥BC,
∴△ADE∽△ACB,
∴$\frac{AD}{AC}$=$\frac{DE}{BC}$,即$\frac{6-x}{6}$=$\frac{x}{8}$,即得x=$\frac{24}{7}$,
即正方形CDEF边长为$\frac{24}{7}$;
方法二:当所截的正方形的边在△ABC的斜边上,如图2,作CM⊥AB于M,交CD于N,
AB=$\sqrt{{6}^{2}+{8}^{2}}$=10,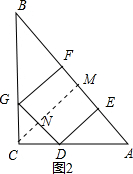 ∵$\frac{1}{2}$CM•AB=$\frac{1}{2}$AC•BC,
∵$\frac{1}{2}$CM•AB=$\frac{1}{2}$AC•BC,
∴CM=$\frac{6×8}{10}$=$\frac{24}{5}$,
设正方形DEFG边长为x,则DG=MNx,CN=$\frac{24}{5}$-x,
∵DG∥AB,
∴△CDG∽△CAB,
∴$\frac{DG}{AB}$=$\frac{CN}{CM}$,即$\frac{x}{10}$=$\frac{\frac{24}{5}-x}{\frac{24}{5}}$,解得x=$\frac{120}{37}$,
∵$\frac{24}{7}$=$\frac{120}{35}$>$\frac{120}{37}$,
∴采用方法一利用率高.
点评 本题考查了相似三角形的应用:先证明三角形相似,然后用相似三角形对应边的比相等的性质求线段的长.也考查了正方形的性质.

| A. | AB=A′B′,BC=B′C′,∠C=∠C′ | |
| B. | ∠B=135°,∠B′=135°,AB=B′C′,BC=C′A′ | |
| C. | AB=BC=CA,A′B′=B′C′=C′A′,∠A=∠A′ | |
| D. | AB=A′B′,BC=B′C′,∠B=∠B′=135° |
| A. | 了解旬河水中汞含量是否符合规定标准 | |
| B. | 了解县师训教研中心36名员工的健康状况 | |
| C. | 商家为了解某一批“电子白板”的使用寿命 | |
| D. | 为了解空气中PM2.5含量 |
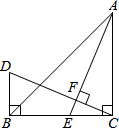 在△ABC中,∠ACB=90°,E是BC边上的一点,过C作CF⊥AE,垂足为F,过点B作BD⊥BC,交CF的延长线于点D,若∠D=65°,求∠EAC的度数.
在△ABC中,∠ACB=90°,E是BC边上的一点,过C作CF⊥AE,垂足为F,过点B作BD⊥BC,交CF的延长线于点D,若∠D=65°,求∠EAC的度数. 如图,AB∥CD,直线EF分别交AB,CD于点E,F,EG平分∠BEF,交CD于点G,如果∠1=108°,求∠2的度数.
如图,AB∥CD,直线EF分别交AB,CD于点E,F,EG平分∠BEF,交CD于点G,如果∠1=108°,求∠2的度数.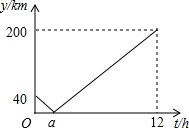 甲、乙两车要从M地沿同一条公路运输一批物资到N地,乙车比甲车先行驶1h,设甲车与乙车之间的距离为y(单位:km),甲车行驶时间为t(单位:h),y与t之间的函数关系如图所示(假设甲、乙两车速度始终保持不变).结合图象解答下列问题:
甲、乙两车要从M地沿同一条公路运输一批物资到N地,乙车比甲车先行驶1h,设甲车与乙车之间的距离为y(单位:km),甲车行驶时间为t(单位:h),y与t之间的函数关系如图所示(假设甲、乙两车速度始终保持不变).结合图象解答下列问题: