题目内容
4.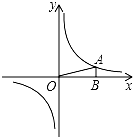 如图,在直角坐标系中,O为坐标原点.已知反比例函数y=$\frac{k}{x}$(k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为$\frac{1}{2}$.
如图,在直角坐标系中,O为坐标原点.已知反比例函数y=$\frac{k}{x}$(k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为$\frac{1}{2}$.(1)求k和m的值;
(2)求当x≥1时函数值y的取值范围.
分析 (1)根据三角形的面积公式先得到m的值,然后把点A的坐标代入y=$\frac{k}{x}$,可求出k的值;
(2)求出x=1时,y的值,再根据反比例函数的性质求解.
解答 解:(1)∵A(2,m),
∴OB=2,AB=m,
∴S△AOB=$\frac{1}{2}$•OB•AB=$\frac{1}{2}$×2×m=$\frac{1}{2}$,
∴m=$\frac{1}{2}$,
∴点A的坐标为(2,$\frac{1}{2}$),
把A(2,$\frac{1}{2}$)代入y=$\frac{k}{x}$,得k=1;
(2)∵当x=1时,y=1,
又∵反比例函数y=$\frac{1}{x}$在x>0时,y随x的增大而减小,
∴当x≥1时,y的取值范围为0<y≤1.
点评 本题考查了反比例函数图象上点的坐标特征,点在图象上,点的横纵坐标满足图象的解析式;也考查了反比例函数的性质,三角形的面积公式以及代数式的变形能力.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
12.给出四个数0,$\sqrt{3}$,π,-1,其中最小的是( )
| A. | 0 | B. | $\sqrt{3}$ | C. | π | D. | -1 |
16.若$\frac{{\sqrt{2x-1}}}{x-3}$在实数范围内有意义,则x的取值范围是( )
| A. | x≠3 | B. | x>$\frac{1}{2}$且x≠3 | C. | x≥2 | D. | x≥$\frac{1}{2}$且x≠3 |
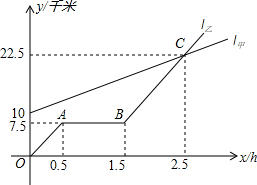 如图,l甲,l乙分别表示甲走路与乙骑自行车(在同一条路上)行走的路程y与时间x的关系,观察图象并回答下列问题:
如图,l甲,l乙分别表示甲走路与乙骑自行车(在同一条路上)行走的路程y与时间x的关系,观察图象并回答下列问题: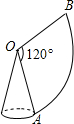 如图,有一圆心角为120°,半径长为6cm的扇形,若将OA、OB重合后围成一圆锥侧面,那么圆锥的高是4$\sqrt{2}$ cm.
如图,有一圆心角为120°,半径长为6cm的扇形,若将OA、OB重合后围成一圆锥侧面,那么圆锥的高是4$\sqrt{2}$ cm.