题目内容
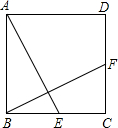 正方形ABCD中,E为BC的中点,F为CD的中点,求证:AE⊥BF.
正方形ABCD中,E为BC的中点,F为CD的中点,求证:AE⊥BF.考点:正方形的性质
专题:证明题
分析:根据题目中给出的条件,易证△ABE≌△BCF,可得∠1=∠3,根据∠2+∠3=90°可以判定∠1+∠2=90°,即∠AGB=90°,∴AE⊥BF.
解答: 证明:在△ABE和△BCF中,
证明:在△ABE和△BCF中,
,
∴△ABE≌△BCF(SAS),
∴∠1=∠3,
又∵∠2+∠3=90°,
∴∠1+∠2=90°,
∠AGB=90°,
即AE⊥BF.
 证明:在△ABE和△BCF中,
证明:在△ABE和△BCF中,
|
∴△ABE≌△BCF(SAS),
∴∠1=∠3,
又∵∠2+∠3=90°,
∴∠1+∠2=90°,
∠AGB=90°,
即AE⊥BF.
点评:本题考查了正方形各边长相等、各内角为直角的性质,全等三角形的判定,全等三角形对应边相等的性质,本题中求证△ABE≌△BCF是解题的关键.

练习册系列答案
相关题目
已知a,b,c均为整数,且满足a2+b2+c2+3<ab+3b+2c.则以a+b,c-b为根的一元二次方程是( )
| A、x2-3x+2=0 |
| B、x2+2x-8=0 |
| C、x2-4x-5=0 |
| D、x2-2x-3=0 |
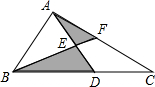 如图,△ABC的面积等于25cm2,AE=ED,BD=2DC.则△AEF与△BDE的面积之和等于
如图,△ABC的面积等于25cm2,AE=ED,BD=2DC.则△AEF与△BDE的面积之和等于