题目内容
如果多项式（x-a）（x+2）-1能够写成两个多项式（x+3）和（x+b）的乘积，那么a= ，b= ．
考点：因式分解的应用
专题：计算题
分析：将多项式（x-a）（x+2）-1与（x+3）（x+b）全部展开，使得对于x的各次项系数对应相等，列出方程组，即可解得a、b的值．
解答：解：由题意得（x-a）（x+2）-1=（x+3）（x+b），
即x2+（2-a）x-2a-1=x2+（3+b）x+3b
∴可得方程组
，
解得a=-2，b=1．
故答案为：-2，1
即x2+（2-a）x-2a-1=x2+（3+b）x+3b
∴可得方程组
|
解得a=-2，b=1．
故答案为：-2，1
点评：本题考查因式分解的应用，解决本题主要运用如果两个多项式相等，必然是对应次项系数相等．
练习册系列答案
相关题目
二次函数y=ax2+bx+c的图象如图所示，则化简二次根式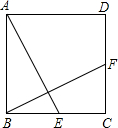
正方形ABCD中，E为BC的中点，F为CD的中点，求证：AE⊥BF．
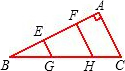如图，Rt△ABC中，