题目内容
10.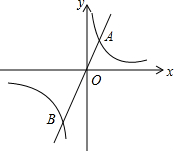 如图,过原点O的直线与双曲线y=$\frac{1}{x}$(x>0)交于点A,与双曲线y=$\frac{k}{x}$(x<0)交于点B.若OB=2OA,则k=4.
如图,过原点O的直线与双曲线y=$\frac{1}{x}$(x>0)交于点A,与双曲线y=$\frac{k}{x}$(x<0)交于点B.若OB=2OA,则k=4.
分析 设直线与双曲线y=$\frac{1}{x}$(x>0)交点横坐标为a,纵坐标为b 由题意得 直线与y=$\frac{k}{x}$的交点坐标为-2a,-2b 因为ab=1,所以2a×2b=4ab=4,根据反比例函数图象上点的坐标特征即可求得k=4.
解答 解:设直线与双曲线y=$\frac{1}{x}$(x>0)交点A的横坐标为a,纵坐标为b,
∴ab=1,
∵OB=2OA,
∴直线与y=$\frac{k}{x}$的交点坐标为-2a,-2b
∴k=(-2a)×(-2b)=4ab=4.
故答案为4.
点评 此题主要考查了反比例函数图象上点的在特征,利用k=xy得出是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.已知m是关于x的方程x2-2x-3=0的一个根,则2m2-4m的值为( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
8.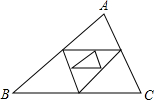 如图,△ABC周长为1,连接△ABC三边中点构成第二个三角形,再连接第二个三角形三边中点构成第三个三角形,以此类推,第2016个三角形的周长为( )
如图,△ABC周长为1,连接△ABC三边中点构成第二个三角形,再连接第二个三角形三边中点构成第三个三角形,以此类推,第2016个三角形的周长为( )
 如图,△ABC周长为1,连接△ABC三边中点构成第二个三角形,再连接第二个三角形三边中点构成第三个三角形,以此类推,第2016个三角形的周长为( )
如图,△ABC周长为1,连接△ABC三边中点构成第二个三角形,再连接第二个三角形三边中点构成第三个三角形,以此类推,第2016个三角形的周长为( )| A. | 22016 | B. | 22017 | C. | ${(\frac{1}{2})}^{2016}$ | D. | ${(\frac{1}{2})}^{2015}$ |
 如图,某轮船在海上以每小时30海里的速度向正西方向航行,上午8:00在点B处测得小岛A在北偏东30°方向,上午9:00船到达C处,测得岛A在北偏东45°方向,如果轮船继续向西航行,上午11:00到达点D处,求点D与小岛A的距离(精确到0.1海里)
如图,某轮船在海上以每小时30海里的速度向正西方向航行,上午8:00在点B处测得小岛A在北偏东30°方向,上午9:00船到达C处,测得岛A在北偏东45°方向,如果轮船继续向西航行,上午11:00到达点D处,求点D与小岛A的距离(精确到0.1海里)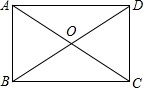 如图所示,矩形ABCD中,对角线AC、BD相交于O,∠ADB=30°,BD=6cm,试求此矩形的周长和面积.
如图所示,矩形ABCD中,对角线AC、BD相交于O,∠ADB=30°,BD=6cm,试求此矩形的周长和面积.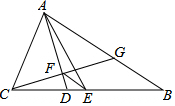 如图,在△ABC中,AB=5,AC=3,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为1.
如图,在△ABC中,AB=5,AC=3,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为1.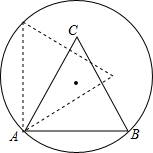 如图,正三角形ABC的边长为1,点A,B在半径为$\frac{\sqrt{2}}{2}$的圆上,点C在圆内,将正三角形ABC绕点A逆时针旋转,当点C第一次落在圆上时,则点C转过的度数为30°.
如图,正三角形ABC的边长为1,点A,B在半径为$\frac{\sqrt{2}}{2}$的圆上,点C在圆内,将正三角形ABC绕点A逆时针旋转,当点C第一次落在圆上时,则点C转过的度数为30°.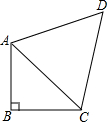 如图,∠ABC=90°,$\frac{AB}{AC}$=$\frac{\sqrt{7}}{4}$,BC=6,AD=DC,∠ADC=60°.
如图,∠ABC=90°,$\frac{AB}{AC}$=$\frac{\sqrt{7}}{4}$,BC=6,AD=DC,∠ADC=60°.