题目内容
8.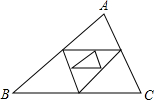 如图,△ABC周长为1,连接△ABC三边中点构成第二个三角形,再连接第二个三角形三边中点构成第三个三角形,以此类推,第2016个三角形的周长为( )
如图,△ABC周长为1,连接△ABC三边中点构成第二个三角形,再连接第二个三角形三边中点构成第三个三角形,以此类推,第2016个三角形的周长为( )| A. | 22016 | B. | 22017 | C. | ${(\frac{1}{2})}^{2016}$ | D. | ${(\frac{1}{2})}^{2015}$ |
分析 根据三角形的中位线定理建立周长之间的关系,按规律求解.
解答 解:根据三角形中位线定理可得第二个三角形的各边长都等于最大三角形各边的一半,
那么第二个三角形的周长=△ABC的周长1×$\frac{1}{2}$=$\frac{1}{2}$,
第三个三角形的周长为=△ABC的周长$\frac{1}{2}$×$\frac{1}{2}$=($\frac{1}{2}$)2,
第2016个三角形的周长═($\frac{1}{2}$)2015.
故选D.
点评 本题考查了三角形的中位线定理,三角形的周长公式,解决本题的关键是利用三角形的中位线定理得到第n个三角形的周长与第一个三角形的周长的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列图形是四种运动品牌的商标,其中是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
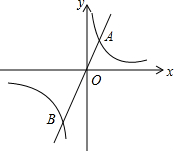 如图,过原点O的直线与双曲线y=$\frac{1}{x}$(x>0)交于点A,与双曲线y=$\frac{k}{x}$(x<0)交于点B.若OB=2OA,则k=4.
如图,过原点O的直线与双曲线y=$\frac{1}{x}$(x>0)交于点A,与双曲线y=$\frac{k}{x}$(x<0)交于点B.若OB=2OA,则k=4. 如图,已知在△ABC中,CD⊥AB于D,BD=9,BC=15,AC=20.
如图,已知在△ABC中,CD⊥AB于D,BD=9,BC=15,AC=20. 如图,在四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°.
如图,在四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°.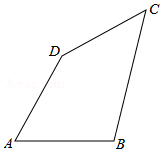 如图,在四边形ABCD中,AB=AD=8,∠A=60°,BC=10,CD=6.
如图,在四边形ABCD中,AB=AD=8,∠A=60°,BC=10,CD=6.